使用 GPT-5 加速科学的早期实验
Early science acceleration experiments with GPT-5
摘要
像 GPT-5 这样的 AI 模型正在成为对科学家越来越有价值的工具,但许多科学家仍然不了解前沿 AI 的能力。我们收集了一系列短案例研究,展示 GPT-5 在数学、物理学、天文学、计算机科学、生物学和材料科学等领域正在进行的研究中产生的新的、具体的进展。在这些案例中,作者们重点介绍了 AI 如何加速了他们的工作,以及它在哪些方面存在不足;AI 在哪些地方节省了专家的时间,以及在哪些地方人类的输入仍然是关键。
我们记录了人类作者与 GPT-5 之间的互动,作为人与 AI 富有成效的协作的指导性范例。值得注意的是,本文包含四个新的数学结果(经人类作者仔细验证),突显了 GPT-5 如何帮助人类数学家解决以前未解决的问题。这些贡献在范围上是适度的,但考虑到前沿 AI 发展的速度,其意义是深远的。
引言
在过去几年中,大语言模型在写作、编程和规划等任务上变得越来越有用。最近,它们已经开始能够为科学研究做出智力贡献。通过 GPT-5,我们看到了一些早期迹象:在专家的指导下,模型可以提出有价值的想法,进行深度文献检索,甚至产生完整的新证明。本报告记录了 GPT-5 为科学进步做出贡献的内部和外部案例,以及它的不足之处。我们的目标是强调当前的可能性,指出仍然遥不可及的目标,以及对科学研究未来的影响。
我们专注于跨越数学、物理学、天文学、计算机科学、生物学和材料科学的具体案例。由于主题差异很大,每个部分都以对背景和动机的解释开始,然后再讨论 GPT-5 做出的贡献。我们尽可能提供 ChatGPT 对话记录,以便清楚地说明模型当前增加价值的地方以及专家监督仍然至关重要的地方。近几个月也出现了几篇类似精神的相关报告,包括 Feldman & Karbasi、Diez 等人、Ivanisvili & Xie、Alexeev & Mixon、Jang & Ryu、Salim,以及 Georgiev、Tao 等人的工作。我们注意到,后者的论文,即 Google 的 AlphaEvolve,风格上略有不同,因为它专注于具有明确定义目标函数的搜索问题,可以通过爬山来解决。相比之下,我们(以及其他引用的论文)专注于可以回答任何类型查询的通用系统。这两种方法是互补的,各自为科学家提供独特的优势。
我们也仔细指出当前 AI 模型的局限性。GPT-5 是不完美的:它可能会自信地犯错,热切地为自己辩护,并在过程中混淆自己(和我们)。结果可能取决于初始提示和后续响应的细节,因此可能难以重现。尽管有这些局限性,我们确实看到了真正的进步。GPT-5 可以搜索广泛的概念空间,整合多样的信息源,并快速迭代。它可以不知疲倦地提出新想法,帮助将模糊的想法转化为具体的结果,并进行理智检查或扩展某一思路。在某些领域,如文献搜索,它往往是独特有效的。
我们的目标不是声称超出证据所允许的范围。而是要用具体的例子展示 GPT-5 今天能做什么和不能做什么,并为研究人员如何使用它加速科学发现提供清晰的路径,同时保持高标准。我们相信 GPT-5 已经为今天的科学研究人员提供了实质性价值,并将在明天成为更强大的工具。本文的其余部分组织如下:
- 第一章收集了 GPT-5 在数学、物理和生物学研究前沿独立重新发现已知结果的案例。
- 第二章突出了 GPT-5 执行"深度文献搜索"的能力。它能够专注于核心概念而非描述这些概念的术语,从而跨越科学学科之间的语言障碍,发现看似被遗忘或难以找到的联系。
- 第三章展示了人类研究人员与 GPT-5 协同工作以加速其研究工作流程的案例。
- 第四章展示了 GPT-5 获得新的研究级别成果的案例。
I. 独立重新发现科学前沿的已知结果
I.1 改进近期凸优化结果中的步长条件 — Sébastien Bubeck
本节可以视为论文其余部分的热身。实验于 2025 年 8 月 20 日进行,当时尚不清楚 GPT-5 是否可以用于推动研究级问题的前沿。本实验的目标比其他几节描述的内容更为温和,仅仅是看看 GPT-5 是否能够重现一篇近期论文的主要结果,具体来说是 [BSZ25] 中的主定理。选择这篇特定论文有几个原因:
- 首先,显然,这篇论文不在 GPT-5 的训练数据中,因为它太新了。但更重要的是,主定理涉及一个非常经典领域(凸优化)的全新问题,特别是在训练数据中找不到任何关于这个问题的痕迹。
- 这篇论文在 arXiv 上有三个版本(v1、v2、v3),关键是 v1 提出了一个次优结果,然后在 v2 中被改进(并达到最优)。我感兴趣的挑战是:给定 v1,GPT-5 能否重新推导出 v2?
- 特别是,如果 GPT-5 能够从 v1 重新推导出 v2,这将表明它本可以反事实地加速科学发现过程。正如我们将看到的,GPT-5 未能完全重新推导出 v2 的结果,但它基本上达到了 v1 和 v2 之间的中间水平。(另见本节末尾关于使用能够进行更长时间推理的模型从头推导 v2 的评论。)
值得注意的是,这是我第一次尝试这类实验(即,除了 [BSZ25] 之外,我没有尝试过任何其他论文)。
I.1.1 问题描述
优化目标函数 $f : \mathbb{R}^d \rightarrow \mathbb{R}$ 的最基本算法是常数步长 $\eta$ 的梯度下降,其中迭代由以下公式给出:
凸优化中的一个经典结果是,对于光滑凸函数,当且仅当步长小于 $2/L$ 时收敛才会发生,其中 $L$ 是光滑常数(即梯度映射 $x \mapsto \nabla f(x)$ 的 Lipschitz 常数)。在 [BSZ25] 中,作者研究了收敛问题的一个新变体,据我们所知(该论文的作者和本文作者),此前从未有人研究过:与其仅仅询问收敛性,不如问在什么条件下被访问的目标函数值本身构成凸曲线,即通过点 $\{(n, f(x_n))\}_{n \in \mathbb{N}}$ 的分段线性函数本身是凸函数?
在论文的 v1 版本中,作者证明了 $\eta \leq 1/L$ 是充分条件,他们还表明 $\eta \leq 1.75/L$ 是必要条件。在 v2 版本中,他们弥合了这个差距,证明了 $\eta \leq 1.75/L$ 确实是充分的。
I.1.2 GPT-5 作为协作者:从 v1 接近 v2
附件:[2503.10138v1.pdf]
你能改进定理 1 中关于步长的条件吗?我不想添加任何新的假设,我只是希望你在定理 1 相同的假设下改进步长条件。
[推理时间 17 分 35 秒]
是的。在与定理 1 相同的假设下(凸 $L$-光滑函数 $f$ 和梯度下降的固定步长),你可以将保证凸性的窗口从 $\eta \leq 1/L$ 扩大到
即,对于任何步长 $\eta \in (0, 3/(2L)]$,优化曲线 $n \mapsto f(x_n)$ 是凸的。这严格改进了定理 1 的界,且仍低于定理 2 所展示的非凸性区域。请参阅定理 1 和定理 2(第 4-6 页)了解下面引用的问题设置和陈述。
如上所述,我感兴趣的实验是:给定 v1,GPT-5 能否重新推导出 v2? 为了检验这一点,我上传了 v1 论文的 PDF,然后简单地要求 GPT-5 (Pro) 尝试改进结果。完整的交互记录在上面的图 I.1 中。特别地,可以看到 GPT-5 声称已将条件从 $\eta \leq 1/L$ 改进到 $\eta \leq 1.5/L$,从而接近最优界(但未完全达到)$\eta \leq 1.75/L$。但这个声明有根据吗?确实有,GPT-5 给出的证明如图 I.2 所示,本文作者已验证其正确性。此外,我检查了推理轨迹以确保没有进行网络搜索(因为这可能会揭示 v2 的存在),而且 GPT-5 给出的证明与 v2 中的证明相当不同。实际上,GPT-5 的证明可以被视为 v1 证明的更标准变体,而(人类的)v2 证明需要对不同不等式进行巧妙的加权以使某些项相消。
直白地说,这样的结果(从 $1/L$ 改进到 $1.5/L$)可能由该领域的某些专家在几小时内实现,而对于大多数专家来说,可能需要几天时间。这就是我们在本报告中将反复看到的科学加速类型。
我们以一个注释结束本节:我们的内部模型可以思考几个小时,能够从头推导出最优界 $1.75/L$(即,无需在上下文中提供论文的 v1,而是直接询问这里研究的主要问题)。
设 $f:\mathbb{R}^d\to\mathbb{R}$ 是凸的且 $L$-光滑的,考虑梯度下降
如果 $\eta\in(0,\tfrac{3}{2L}]$,则序列 $\{f(x_k)\}_{k\ge 0}$ 是凸的,即减少量
构成一个非递增序列:对所有 $k\ge 0$,$D_{k+1}\le D_k$。
记 $g_k:=\nabla f(x_k)$ 且 $\Delta_k:=g_{k+1}-g_k$。我们比较两个连续的减少量 $D_k$ 和 $D_{k+1}$。
(1) $D_k$ 的下界。 对于凸 $L$-光滑函数 $f$,Bregman 散度满足
取 $x=x_k$,$y=x_{k+1}$ 且 $x_k-x_{k+1}=\eta g_k$,得到
(2) $D_{k+1}$ 的上界。 由凸性,$f(x)-f(y)\le \langle \nabla f(x),x-y\rangle$。取 $x=x_{k+1}$,$y=x_{k+2}$ 且 $x_{k+1}-x_{k+2}=\eta g_{k+1}$,
(3) 相减并使用共强制性。 从 (A) 减去 (B) 得到
由于 $g_{k+1}=g_k+\Delta_k$,我们有 $\langle g_{k+1},\Delta_k\rangle=\langle g_k,\Delta_k\rangle+\|\Delta_k\|^2$,因此
对于凸 $L$-光滑函数 $f$,梯度是 $1/L$-共强制的:
因此,
如果 $\eta\le \tfrac{3}{2L}$,右侧非负,所以对所有 $k$ 有 $D_{k+1}\le D_k$,这等价于序列 $\{f(x_k)\}_{k\ge 0}$ 的凸性。∎
I.2 用 GPT-5 发现新的黑洞对称性 — Alex Lupsasca
我们以标准化格式记录了一项由 AI 执行的黑洞物理学理论计算。GPT-5 Pro(重新)推导了静态、轴对称波动方程在 Kerr 背景上的非平凡 Lie 点对称性——包括一个 $\mathsf{SL}(2,\mathbb{R})$ 代数。该模型最初在弯曲空间问题上失败了,但在平空间热身后成功了,最终产生了支撑 [Lup25] 中最新结果的正确对称性生成元(模型无法访问该论文)。
I.2.1 问题背景
天体物理黑洞由其质量 $M$ 和角动量 $J=aM$ 表征。这两个量完全决定了黑洞时空几何:它由参数为 $(M,a)$ 的 Kerr 度规描述。
我们研究旋转(Kerr)黑洞上的无质量、静态、轴对称波。在 Boyer-Lindquist 坐标 $(t,r,x,\phi)$(其中 $x=\cos\theta$)中,控制方程是受限于这些对称性的标量 Laplace 算子,
这是一个关于两个变量的线性二阶偏微分方程。它的解编码了黑洞的静态潮汐响应;它们的渐近行为决定了视界可变形性("Love 数")。在广义相对论中,黑洞表现出消失的(静态)Love 数,这种令人惊讶的刚性通常被追溯到场方程的隐藏对称性。
因此,一个关键问题是:方程 (I.1) 的对称性是什么?
人类方法。 经典地,人们会对方程 (I.1) 应用 Lie 的降阶算法。在这个过程中,首先假设一个对称性生成元 $X=\xi^r\partial_r+\xi^x\partial_x+\eta\partial_\psi$,将 $X$ 延拓到导数,然后施加方程 (I.1) 的不变性,最后求解关于未知函数 $(\xi^r,\xi^x,\eta)$ 的超定系统。这在弯曲黑洞背景中是艰巨的(系数通过 $\Delta$ 和 $1-x^2$ 依赖于 $r$ 和 $x$)。在最近的工作 [Lup25] 中,我进行了这项分析,惊讶地发现三个生成 $\mathsf{SL}(2,\mathbb{R})$ 代数的非平凡 Lie 点对称性。这些对称性包括与尺度不变性相关的膨胀 $H_0$,可用于解释广义相对论中黑洞潮汐响应(消失的 Love 数)的缺失。
I.2.2 给 GPT-5 Pro 的任务:目标、提示和模型行为
目标。 从 GPT-5 Pro 引出方程 (I.1) 的 Lie 点对称性,理想情况下重现 [Lup25] 中最近获得的 $\mathsf{SL}(2,\mathbb{R})$ 生成元及其弯曲空间系数。
结果。 经过约 5 分钟的内部推理后,模型(错误地)报告该方程除了平凡的缩放外没有连续对称性。
PDE (I.1) 的 Lie 点对称性是什么?
[推理时间 5 分 13 秒]
[错误答案:GPT-5 Pro 找不到对称性,并错误地断言不存在对称性。]
热身提示和结果(在平空间上成功)。 为了搭建脚手架,我们初始化了模型的新实例,首先在柱坐标 $(\rho,z)$(其中 $\rho=r\sqrt{1-x^2}$,$z=rx$)下提出平空间极限 $M,a\to0$:
结果。 经过 10 分 27 秒后,模型产生了所有对称性,包括生成 $\mathsf{SL}(2,\mathbb{R})$ 的三个:
这里 $H_-$ 是非平凡的特殊共形生成元;获得它表明模型执行了(或模拟了)真正的对称性计算,而不是猜测。
(I.2) 的 Lie 点对称性是什么?
[推理时间 10 分 27 秒]
[正确答案,包括生成元 (I.3)。]
(I.1) 的 Lie 点对称性是什么?
[推理时间 18 分 9 秒]
[正确答案,包括生成元 (I.4)。]
第二次弯曲空间尝试和结果(成功)。 然后我们给同一个 GPT-5 实例相同的提示:"(I.1) 的 Lie 点对称性是什么?"
结果。 在约 18 分钟内,模型产生了正确的弯曲空间生成元,构成 $\mathsf{SL}(2,\mathbb{R})$:
I.2.3 结果、影响和后续步骤
分析。 总之,以下是:
- GPT-5 做对的:相对简单的平空间对称性;完整的非平凡弯曲空间系数;$\mathsf{SL}(2,\mathbb{R})$ 结构。
- GPT-5(在过程中)做错的:对方程 (I.1) 的冷启动错误地得出"无对称性"的结论。模型似乎需要通过更简单的平空间问题 (I.2)(具有相同的对称性结构)进行"热身"。
结果。 GPT-5 Pro(重新)发现了方程 (I.1) 的弯曲空间 $\mathsf{SL}(2,\mathbb{R})$ 对称性生成元 (I.4)。这与 [Lup25] 的关键结构性洞见相匹配。实际上,一旦知道对称性,下游结果(例如,潮汐响应的约束和该扇区中静态 Love 数的消失)就可以通过相对适度的分析得出。
对交互的反思。 两个观察:
- 脚手架很重要。模型"冷启动"失败但在密切相关的热身后迅速成功。这表明检索或内部模式激活可以通过呈现同一对称性类的更简单成员来启动。
- 算法合理性。最终的生成元结构太复杂,不可能是幸运的猜测。模型可能(隐式地)执行了以下组合:识别平坦方程中的共形不变性,假设弯曲类似物,和/或利用将方程 (I.1) 简化为方程 (I.2) 的坐标映射。
影响。
- AI 作为对称性引擎。通过最少的领域脚手架,当前模型可以对具有非常数系数的 PDE 进行非平凡的 Lie 对称性发现。
- 研究速度。鉴于这些能力,一旦正确的提示和脚手架就位,从想法到可发表结果的时间可以从几个月压缩到几天。
- 泛化机会。相同的工作流程(在简化问题上热身,然后提升)可以应用于黑洞理论及更广泛领域中更复杂的物理问题。
要点。 GPT-5 Pro 在适当搭建脚手架后,揭示了黑洞潮汐响应核心弯曲空间 PDE 的 $\mathsf{SL}(2,\mathbb{R})$ 对称性内容。这支持了一个更广泛的论点:当代 LLM 可以作为理论物理中对称性发现和解析结构挖掘的实用助手。
I.3 使用 GPT-5 Pro 进行体外免疫系统实验的机制分析和结果预测 — Derya Unutmaz 医学博士
在这里,我展示了 GPT-5 Pro 成功分析了一张关于人类 T 细胞与 2-脱氧-D-葡萄糖 (2-DG) 培养实验的图片,该实验显示促炎性 Th17 细胞亚群增加。这个实验是我们实验室几年前进行的,但机制仍不清楚。GPT-5 Pro 提供了可以解释这些发现的关键机制,此外还提出了高度相关的实验建议。尽管我们在该领域具有深厚的专业知识,但这些机制洞见和进一步解剖这些发现的假设非常有价值且并非立即显而易见。
在随后的一张未发表的图中,GPT-5 Pro 解释了短暂糖酵解抑制后细胞毒性 T 细胞上检查点抑制剂 PD-1 和 LAG-3 的流式细胞术数据,推断 2-DG 通过对糖基化的综合影响以及通过减弱的 T 细胞受体信号传导来重编程抑制性受体表达。它进一步正确预测,在这些细胞的 CAR-T 细胞生成过程中短暂的 2-DG 脉冲会增强它们对靶癌细胞系的细胞毒性,这一点我们已在未发表的结果中内部验证。总之,这些例子说明了 GPT-5 Pro 如何能够作为生物医学研究中真正的机制共同研究者,将数月的推理压缩为几分钟,发现非显而易见的假设,并直接塑造可实验测试的策略。
I.3.1 问题背景
我们一直在研究称为 T 细胞的人类免疫细胞亚群如何响应其葡萄糖代谢的修改。有大量证据表明,葡萄糖摄取和能量代谢影响 T 细胞分化为效应亚群,这可以增强对感染的保护或驱动慢性炎症和自身免疫等病理,并可能对癌症免疫治疗产生影响。为了解剖这一机制,我们使用葡萄糖的竞争性类似物 2-脱氧-D-葡萄糖 (2-DG) 作为 T 细胞葡萄糖摄取的抑制剂。由于 T 细胞高度异质,我们首先将其分选为 CD4⁺ 和 CD8⁺ 亚群,分别是辅助性和细胞毒性 T 细胞。在最初的实验中,我们使用 CD4⁺ T 细胞并在不同剂量的 2-DG 或低葡萄糖条件下激活它们。两天后,这些处理被洗掉,允许 T 细胞在白细胞介素-2 (IL-2)——一种生长因子细胞因子——的存在下增殖。这个想法是,葡萄糖抑制的任何影响都会在实验早期发生,在启动过程中被印记,并在两周的扩增后表现为 T 细胞分化和功能的差异。
I.3.2 给 GPT-5 的任务:目标、提示和模型行为
下面提示中的图片来自用 2-DG 培养的细胞的流式细胞术数据。我将其作为提示的一部分上传,这导致了与 GPT-5 的以下对话。虽然我们已将类似的发现作为预印本发表,但这个特定的图或实验之前没有发表过。
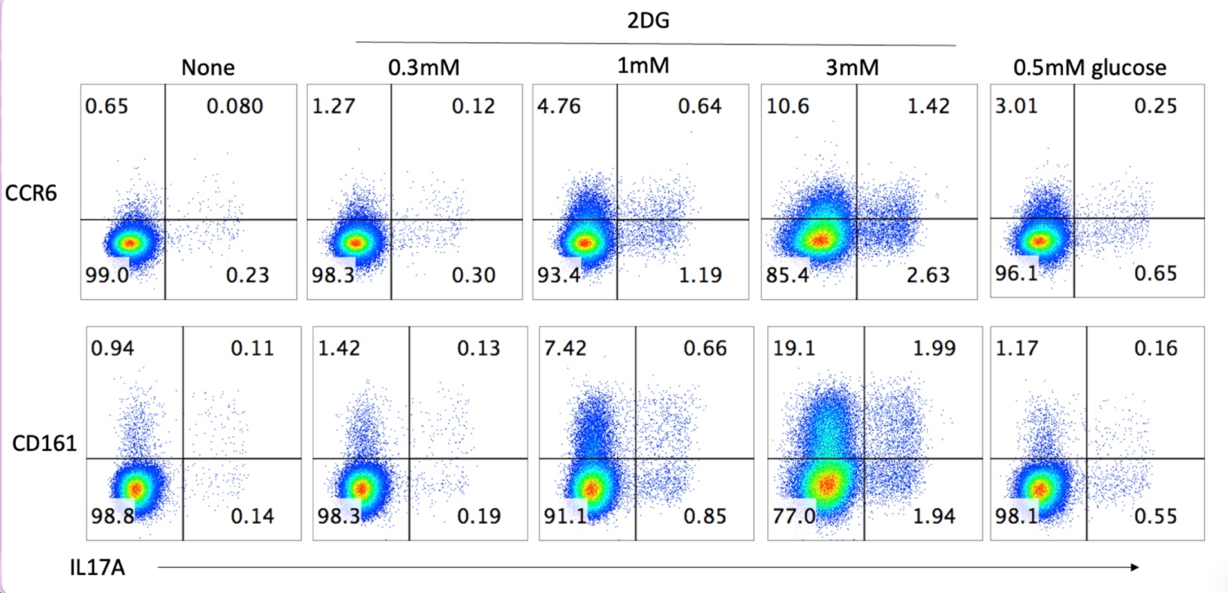
图 I.3:用于分析的 T 细胞流式细胞术数据
[上传上图]
背景和问题:我们测试了人类 T 细胞启动期间短暂的糖酵解抑制如何影响后来的 Th17 功能。分选的 CD4⁺ T 细胞在指定浓度的 2-脱氧-D-葡萄糖 (2-DG) 存在下用抗 CD3 和抗 CD28 刺激。然后细胞在没有 2-DG 的情况下扩增两周,重新刺激,并与 CCR6 或 CD161 一起检测 IL-17A。分析在用 PMA 加离子霉素刺激这些培养两周的细胞 6 小时后获得的流式细胞术数据集,然后进行细胞内 IL-17A 染色和 CCR6 及 CD161 的表面染色。解释结果,推导机制,提取高层结论,评估影响,并推荐后续实验。
[推理时间 17 分钟]
在第一次激活期间短暂暴露人类 CD4⁺ T 细胞于 2DG 会留下持久的、剂量依赖的印记,两周后可检测到:IL-17A⁺、CCR6⁺ 和 CD161⁺ 细胞的频率都上升,最大增幅出现在 3mM 2DG。标记物增加(CCR6、CD161)明显大于 IL-17A 本身的增加,这意味着 Th17 谱系记忆(CCR6⁺/CD161⁺)的扩增或印记已准备好但未统一执行 IL-17A 产生。低葡萄糖对照(0.5 mM)部分模拟了这种效果但比相同标称浓度的 2DG 弱,这表明糖酵解限制和 N-连接糖基化干扰(已知的 2DG 脱靶效应)都有贡献,而不仅仅是能量限制。该效果在药物洗脱后持续存在,表明细胞重编程、Th17 谱系细胞的选择性存活/扩增,或两者兼有。
经过 17 分钟的推理,GPT-5 Pro 产生了多个直方图图像,如下面这两个例子,完美地分析了数据,并附有出色的执行摘要,捕捉了关键的机制要点。
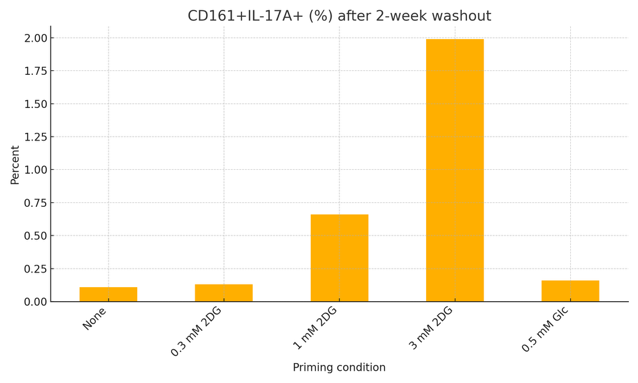
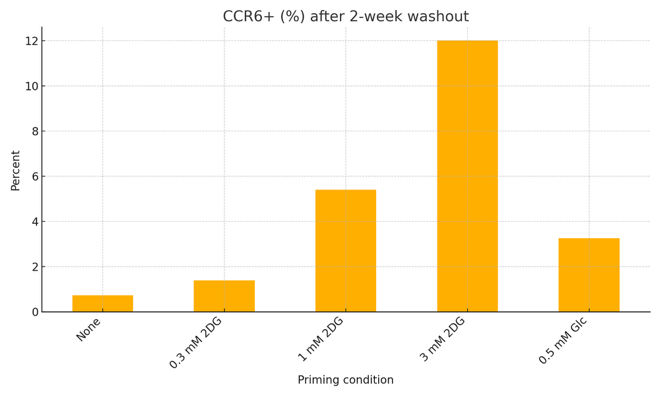
图 I.4:GPT-5 Pro 生成的定量分析直方图
它还生成了该图的定量剂量-响应读数(输出未显示)和包含用于生成直方图的所有基础数据的 CSV 文件。GPT-5 Pro 然后提供了关于 2-DG 处理如何改变 Th17 生物学的解释。GPT-5 Pro 的机制推断是关键性的,其中一些是我们之前没有考虑过的想法。回顾起来,特别是通过干扰 N-连接糖基化减少 IL-2 信号传导的提议机制非常有生物学意义,因为它可以直接解释 2-DG 处理下 Th17 细胞分化的去抑制。然而,这个机制假设之前没有出现在我们脑海中,因为建立这种联系并不立即显而易见。其他机制假设也高度相关且合理。
数据说明:
单次 2DG 暴露在启动时导致两周后:(i) IL-17A⁺ 细胞增加 13 倍,(ii) Th17 谱系标记物(CCR6、CD161)增加 16-20 倍,(iii) CCR6⁺/CD161⁺ 细胞比 IL-17A⁺ 细胞不成比例地更多。这种模式符合 Th17 谱系记忆的富集和/或印记,而不是所有细胞急性效应细胞因子输出的统一增益。许多 CCR6⁺/CD161⁺ 细胞在重新刺激时是 IL-17A⁻,这是准备好的 Th17 记忆的标志,在正确的信号下(例如 IL-1β + IL-23)可以产生 IL-17A。
机制推断。几个非排斥性机制可以产生这种持久的偏斜:
- 通过 N-连接糖基化干扰减少 IL-2 信号传导。毫摩尔级别的 2-DG 扰乱 N-聚糖合成,在激活的 T 细胞中减少糖蛋白的正确表面表达——包括 IL-2Rα (CD25)。减弱的 IL-2/STAT5 信号传导去抑制 Th17 分化并限制 Th17 细胞向 Th1 样状态的转化。2DG 比低葡萄糖效果更强支持糖基化在 ATP/丙酮酸限制之外的作用。
- 锁定谱系程序的急性代谢检查点。短暂的糖酵解抑制可以将激活代谢转向线粒体氧化,改变 mTORC1/HIF-1α 活性和染色质修饰剂(乙酰辅酶 A、α-酮戊二酸),在 Th17 相关位点(RORC、IL-23R、CCR6)留下表观遗传记忆。洗脱后的持续性与这种程序最一致。
- 选择性存活/扩增。2DG 可能优先限制非 Th17 亚群(如 Th1)的增殖或存活,有效富集分选的总 CD4⁺ 池中预先存在的 CCR6⁺/CD161⁺ 记忆。CD161/CCR6 比 IL-17A 更大的倍数增加支持这个解释至少是一个贡献者。
- 改变的 TCR/CD28 信号强度。扰乱的糖基化也会在启动期间调节 TCR 和共刺激受体功能。较弱的 IL-2 富集效应程序和保留的 RORγt/AHR 程序会倾向于 Th17 谱系。
高层结论和潜在影响:启动期间的一次性代谢扰动在人类 CD4⁺ T 细胞中印记了持久的 Th17 倾向记忆表型。由于 Th17/Tc17 状态可以显示出优越的持久性和组织运输,这种印记可能对过继性 T 细胞疗法(包括 CAR-T)有用,当需要 Th17 样程序时。相反,它警告说,短暂的糖酵解抑制——无论是有意的(例如,2-DG 作为抗代谢物)还是偶然的(生物反应器中的营养限制)——可能增加 Th17 谱系记忆,从而如果在体内应用可能加剧 Th17 介导的自身免疫。洗脱后的明显持续性表明我们看到的不是急性代谢抑制,而是有生物学意义的重编程。
GPT-5 Pro 然后提出了关键的后续实验。我们已经在第一次实验几周后进行了第一个实验,即甘露糖挽救实验。结果与 GPT-5 Pro 的预测完全一致。
为了区分机制并建立因果关系,最有信息量的下一步是:
区分"糖酵解阻断"与"糖基化阻断"。重复启动步骤:
- 2-DG ± 甘露糖挽救(恢复 N-糖基化而不恢复糖酵解)
- 不抑制 N-糖基化的特异性糖酵解抑制剂(例如,PFKFB3 抑制剂 3PO 或仔细滴定的非毒性剂量的碘乙酸),以及
- 低剂量的 N-糖基化抑制剂(例如,衣霉素)。如果甘露糖逆转 2-DG 效应而仅糖酵解抑制剂不能表型复制它,则糖基化是驱动因素。
在启动期间询问 IL-2 轴。量化表面 CD25 成熟(PNGase F 移位)、pSTAT5 和 IL-2 消耗。用外源 IL-2 或强制 STAT5 信号传导的 IL-2/抗 IL-2 免疫复合物进行挽救实验,如果 IL-2 通路抑制是因果的,应该抵消 Th17 偏斜。
追踪增殖/存活和组成。使用 CellTrace/Ki67 和 Annexin V 在启动后 24-96 小时确定 2-DG 是否通过选择性生长/存活富集 CCR6⁺/CD161⁺ 细胞。包括绝对细胞计数以便解释百分比。
定义表观遗传印记。在启动 ± 2-DG 后和第 14 天再次对 RORC、IL-17A/F、IL-23R、CCR6 和 PRDM1 进行 ATAC-seq 和靶向 CUT&Tag(H3K27ac/H3K4me3)。持久的染色质可及性增益将确认程序化记忆。
I.3.3 CD8⁺ T 细胞和 CAR-T 预测
然后我上传了一张未发表的流式细胞术图片,显示 2-DG 对激活的 CD8⁺ 幼稚和记忆 T 细胞上检查点抑制剂 PD-1 和 LAG-3 的影响(下图)。GPT-5 Pro 完美地分析和描述了图中的数据:
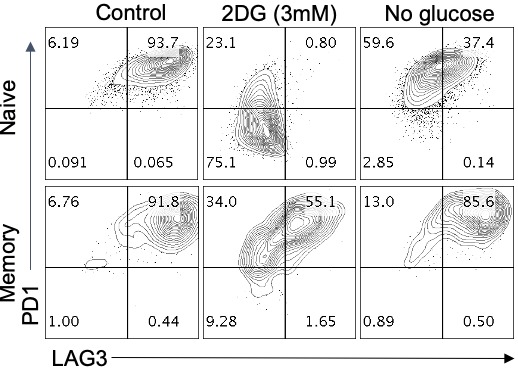
图 I.5:幼稚和记忆 CD8⁺ T 细胞在指定条件下激活后第 4 天 PD-1 和 LAG-3 表面表达的代表性流式细胞术图
在抗 CD3/CD28 激活期间短暂暴露于 3 mM 2-DG 深刻重塑了第 4 天测量的人类 CD8⁺ T 细胞上的早期检查点受体表达。在幼稚 CD8⁺ 细胞中,2-DG 将 PD-1⁺ LAG-3⁺ 群体从约 94% 对照降至约 0.8%,使大多数细胞呈双阴性。在记忆 CD8⁺ 细胞中,2-DG 强烈降低 LAG-3(从约 92% 降至约 57% LAG-3⁺)并将双阳性亚群降至约 55%,总 PD-1⁺ 仅适度降低(从约 99% 降至约 89%)。在无葡萄糖培养基中(糖酵解限制但无糖基化阻断),幼稚细胞仅显示 LAG-3 部分降低(至约 38%)且 PD-1 几乎无变化;记忆细胞基本不变。因此,2-DG 的效果远强于葡萄糖剥夺,与 N-连接糖基化受损而非能量短缺一致。
重要的是,我要求 GPT-5 Pro 模拟一个实验,在该实验中我们会用抗 CD19 CAR 分子对这些 CD8⁺ T 细胞进行基因工程改造以靶向 CD19⁺ 淋巴瘤,并预测先前的 2-DG 处理会如何影响这些细胞对癌细胞的细胞毒性。因为我们已经进行了这个实验(也是未发表的),我能够验证 GPT-5 Pro 的预测,它在预测细胞毒性会增强方面几乎是完美的。
这对抗 CD19 CAR 记忆 CD8⁺ 细胞的预测(模拟)
记忆 CD8⁺ 细胞被激活、用抗 CD19 CAR 转导、在 IL-2 中扩增 2 周、洗去药物,然后与 CD19⁺ 淋巴瘤细胞共培养 3 天。结果读取为特异性裂解和连续杀伤能力。为了分离功能差异,分析门控于 CAR⁺ 细胞,以控制 2-DG 对转导效率的任何影响。
应用于 CAR-T 背景的机制预期:2-DG 脉冲在第 4 天产生较低的 LAG-3 和适度较低的 PD-1,这通常转化为重复靶标遭遇时较少的激活诱导功能障碍。虽然急性糖酵解支持即时的细胞毒性脱颗粒,但你的暴露是短暂的,发生在检测前两周;代谢能力应该恢复,而早期印记的检查点/谱系程序被保留。因此,24 小时的初始杀伤可能相似或略低,但 72 小时的累积杀伤应该在 2-DG 启动下更高,特别是在低 E:T 比率下。
I.3.4 本案例研究的关键要点和影响
总之,GPT-5 Pro 基于我们的实验数据提供了卓越的关键洞见和假设。如果我们在数据分析时就有了 GPT-5 Pro 的这些解释和推荐的下一步实验计划,我们会在几分钟内解决或假设机制洞见。重要的是,尽管我们在该领域具有深厚的专业知识,我们仍然错过了 GPT-5 Pro 提供的关键洞见。此外,GPT-5 Pro 建议了我们发表这些发现所需进行的几个实验,这是共同研究者级别的贡献。更具体的要点和影响是:
- 复杂生物学的精确解释。GPT-5 Pro 快速将观察到的表型与区分糖酵解阻断和受损 N-连接糖基化的机制假设联系起来,提出 IL-2 受体通路作为驱动因素,并预测记忆而非幼稚 T 细胞携带该效应。
- 在实验室中经得起检验的可测试下一步。GPT-5 Pro 产生了一个清晰的实验决策树,包括恢复糖基化的甘露糖挽救、代谢读数和表观遗传检测。这表明该模型可以生成可在湿实验室中测试的高度相关假设。
- 避免错误路径的机制优先思维。通过分离选择效应和程序效应,并提出将糖基化与能量限制分开的对照,GPT-5 Pro 降低了追逐有吸引力但可能不必要的实验的风险,这会浪费许多月的测试。
- 细胞疗法的 AI 引导生物工程。通过正确预测启动期间短暂的 2-DG 暴露会降低 PD-1/LAG-3、保留细胞毒性潜力并增强抗 CD19 CAR 记忆 CD8⁺ T 细胞的连续杀伤,GPT-5 Pro 说明了基础模型如何能够提出具体的、可测试的调整来改进 CAR-T 细胞开发方案,通过在计算机中快速迭代各种条件,然后进行湿实验室验证,从而增强对癌症或自身免疫疾病的治疗性能。
- 对生物医学的长期影响。随着像 GPT-5 Pro 这样的模型成为实验室操作系统的原生组成部分,我们应该期待:跨免疫学、肿瘤学和代谢领域更快的机制发现;由于失败的分支在计算机中被修剪而更便宜的阴性结果;由于选择更好的假设和设计良好的实验方法而更可重复的科学。净效果将是每次实验更高的发现率和从观察到发现到干预的更短路径,从而深刻加速生物医学科学过程。
II. 深度文献搜索
II.1 从密度估计和凸几何到多目标优化 — Nikita Zhivotovskiy
这里讨论的实验最初可追溯到 2025 年 8 月下旬,在随后一些应用更广泛传播之前。目标是应用 GPT-5 不是为了获得直接的文献答案,而是看看一个新证明的几何陈述是否会立即浮现出相邻的文献和应用。这对作者很有用,因为合理的扩展并不清晰,否则需要询问许多专家(以及运气)才能找到正确的联系。
我们从这个实验得出的初步结论是,仅给定一个核心数学陈述,GPT-5 可以快速浮现跨领域的非平凡且技术上一致的联系(这里是多目标优化和近似 Pareto 集),为新应用提供背景。
首先,我们记录激发这个实验的陈述。设 $K$ 是 $\mathbb{R}_+^d$ 的紧子集,$\alpha \ge 1$。如果对于每个 $\theta=(\theta_1,\ldots,\theta_d)\in K$,存在 $\phi=(\phi_1,\ldots,\phi_d)\in A$ 使得对所有 $j=1,\ldots,d$ 有 $\theta_j \le \alpha\,\phi_j$,则称 $K$ 的子集 $A \subset K$ 是 $K$ 的 $\alpha$-比率覆盖。
对于每个 $d \ge 1$ 和每个凸紧集 $K \subset \mathbb{R}_+^d$,存在一个至多有 $2^{8d}$ 个元素的子集 $A \subset K$,它是 $K$ 的 $32$-比率覆盖。
注意 GPT-5 没有参与上述结果的证明。定理 II.1.1 的原始动机是混合物的密度估计统计问题。设 $\{f_1,\ldots,f_d\}$ 是 $\mathbb{R}^p$ 上的密度,对于混合权重 $\theta\in K\subset \Delta^{d-1}$(其中 $\Delta^{d-1}=\{\theta\in\mathbb{R}_+^d:\sum_{i=1}^d \theta_i=1\}$),考虑混合物 $p_\theta(x)=\sum_{i=1}^d \theta_i f_i(x)$。如果 $A$ 是 $K$ 的 $\alpha$-比率覆盖,则对于任何 $\theta\in K$ 存在 $\phi\in A$ 使得 $\theta\le \alpha\,\phi$ 逐坐标成立;因此,$p_\theta(x)\le \alpha\,p_\phi(x)$ 对所有 $x$ 成立,从而 $\frac{p_\theta(x)}{p_\phi(x)}\le \alpha$ 逐点成立,特别地,$\mathrm{KL}(p_\theta\|p_\phi)\le \log \alpha$。这有助于 $\{p_\theta:\theta\in K\}$ 的基于 KL 散度的覆盖界。
当获得定理 II.1.1 形式的结果时,人们自然会问它是否已知以及它适用于哪里。一旦作者有了定理 II.1.1,GPT-5 能够帮助浮现将范围扩展到理论计算机科学的相关结果。
[将定理 II.1.1 及前面的段落放入上下文。]
有哪些类似的已知定量结果?列出不同领域(几何、统计)中最相关的结果。为参考/主题制作一个重要/核心论文的简短列表。
[推理时间 8 分 4 秒]
[...]
你的"$\alpha$-比率覆盖"本质上是多准则优化中使用的(乘法)$\varepsilon$-近似 Pareto 集概念(每个坐标上达到 $(1+\varepsilon)$ 因子的支配)。
- Papadimitriou–Yannakakis (FOCS 2000)。引入了现代框架:多项式大小的 $(1+\varepsilon)$-近似 Pareto 集存在且可计算的条件;乘法逐坐标覆盖的基础。
- [...]

图 II.2:[PY00] 中与定理 II.1.1 密切相关的结果
如图 II.1 所示,在一系列其他相关结果中,2025 年 8 月的交流突出强调了 [PY00] 关于多目标优化的开创性工作。乍一看(见图 II.2),这似乎与定理 II.1.1 无关,可能被误认为是幻觉。然而,解开他们的证明表明,他们的结果可以表述为在 $K\subset[1/R,R]^d$ 上大小为 $O\left((\log R/\varepsilon)^{d-1}\right)$ 的逐坐标 $(1+\varepsilon)$-比率覆盖。相比之下,在 $K$ 的凸性假设下,定理 II.1.1 产生常数因子 $32$ 和与 $R$ 无关的大小界 $2^{8d}$。在 Papadimitriou-Yannakakis 框架中,$K$ 表示可实现的目标向量集;一般不假设凸性(尽管凸实例确实出现)。
[PY00] 的大部分内容致力于构造近最优的 $\varepsilon$-近似 Pareto 集。受这种联系的启发,我们将定理 II.1.1 扩展到大小为 $O\big((\log(1/\varepsilon)/\varepsilon)^{d-1}\big)$ 的 $(1+\varepsilon)$-覆盖,对于凸 $K$,它与范围参数 $R$ 无关。因此,在凸实例中,这从经典的 $O\big((\log R/\varepsilon)^{d-1}\big)$ 界中移除了 $\log R$ 因子,并为凸多目标优化提供了基准。
II.2 Erdős 问题(第 1/2 部分)— Mehtaab Sawhney 和 Mark Sellke
II.2.1 引言
Paul Erdős 是一位多产的数学家,其数学影响横跨数学的多个领域,包括组合学、数论和分析。除了发表超过 1500 篇数学论文外,Erdős 还提出了大量数学猜想,其中一些成为数学中的核心问题。
最近,Thomas Bloom 创建了一个 Erdős 问题的在线索引,这极大地促进了识别和解决这些问题的过程,并为众多在线协作打开了大门。大语言模型在我们故事中的作用实际上始于 2024 年初网站的创建,该网站依赖 ChatGPT 的早期版本帮助编写底层代码。每个列出的问题都有自己的网页,包含状态(大致为"开放"或"已解决")以及用于潜在协作的讨论帖。截至 2025 年 10 月 31 日,该列表持续增长,在 1105 个问题中有 685 个"开放"问题;Erdős 多年来提出的问题分散在许多杂乱的来源中。不幸的是,解决方案通常也同样分散,因此确定一个特定问题是否真的开放,还是几十年前就已解决并被大多数数学家遗忘,可能非常具有挑战性。
我们讨论使用 GPT-5 改进该数据库状态的成功尝试,这导致了以下进展:
- 定位到之前未标记为已知的 10 个问题的已发表解决方案:223、339、494、515、621、822、883(第 2/2 部分)、903、1043、1079。
- 报告现有文献中另外 10 个问题的值得注意的部分进展:32、167、188、750、788、811、827、829、1017、1011。
- 纠正问题 1041 陈述中的一个印刷错误。
- 为问题 #848 生成一个新想法,该想法与在线评论者 van Doorn、Weisenberg 和 Cambie 之前的建议一起,使我们能够解决该问题。
在本节中,我们重点介绍上述前两点中的几个例子。问题 #848 及其解决方案将在后面的第 IV.1 节中介绍。
II.2.2 文献搜索
Erdős 问题数据库作为 GPT-5 能力的测试平台。对于每个列为"开放"的问题,我们要求 GPT-5 定位解决方案(如果存在),否则报告值得在网站上提及的重要部分进展。这是使用 ChatGPT 界面、OpenAI API 和内部 OpenAI 工具的组合完成的;后两者允许并行自动查询许多问题,以及使用 GPT-5 自动过滤响应。
提供的参考资料通常准确且易于手动验证。我们没有观察到 GPT-5 假装找到正确参考资料的情况(尽管在某些情况下它对发现的部分进展过于热情)。
数学家试图查找文献的典型做法要么是沿着长长的参考链,要么试图"猜测正确的搜索短语",希望找到相关文献。使用 GPT-5,人们可以跳过这个人为的中间步骤,直接输入陈述!此外,在数学实践中,人们经常需要在一个单独的领域中定位"肯定存在"的文献;GPT-5 可以根据通常模糊的描述或候选"定理"陈述来做到这一点。
我们重点介绍几个代表性案例。第一个是问题 #339,其令人惊讶的成功是我们努力的动力。
问题 #339([EG80]):设 $A\subseteq \mathbb{N}$ 是阶为 $r$ 的加法基,即每个足够大的整数是 $A$ 中至多 $r$ 个元素之和。可表示为 $A$ 中恰好 $r$ 个不同元素之和的整数集是否必须具有正下密度?(即,对于所有足够大的 $N$,这个集合是否必须占据 $\{1,2,\dots,N\}$ 中整数的非消失分数?)
搜索参考文献的一个困难是,问题 #339 出现在 Erdős-Graham 的一篇 100 页论文 [EG80] 中,该论文列出了许多其他问题,并有大约 700 次引用。对人类来说,整理出哪些与上述特定问题相关将极其耗时。然而,GPT-5 Pro 能够在我们尝试的第一个查询中找到解决方案,仅给出问题网页的截图。
II.2.3 更多示例
这里我们呈现三个更多的例子,进一步说明数学文献搜索中存在的挑战。
问题 #515([Erd61]):设 $f(z)$ 是一个整函数,不是多项式。是否存在一条趋向无穷大的路径 $\gamma$,使得对于每个 $\lambda>0$,积分 $\int_{\gamma} |f(z)|^{-\lambda} dz$ 是有限的?
问题 #750 的部分结果([Erd69]):固定 $\varepsilon>0$。是否必须存在一个具有无限色数的图 $G$,使得每个 $m$ 顶点子图都有一个至少包含 $(\frac{1}{2}-\varepsilon)m$ 个顶点的独立集?
问题 #1043([Erd58]):设 $f\in\mathbb{C}[x]$ 是一个首一多项式。是否必须存在一条直线 $\ell$,使得 $\{z:|f(z)|\leq 1\}$ 在 $\ell$ 上的投影长度至多为 $2$?
GPT-5 分别在 [LNT84]、[EBL82]、[Pom61] 中定位到了解决上述问题的参考文献。识别这些几十年前的论文需要 GPT-5 远远超越搜索引擎的功能,实际上需要详细阅读这些论文并应用对数学的真正理解。
在第一种情况下,[LNT84] 实际上证明了比问题 #515 陈述更一般的内容。即,作者研究 $e^{-F(z)}$ 的积分,其中 $F:\mathbb{C}\to\mathbb{R}$ 是一个次调和函数,意味着它在任何圆上的平均值小于其在圆心处的值。$F(z)=\log |f(z)|$ 在 $f$ 是整函数时是次调和的,这是一个经典事实,这意味着 [LNT84] 的结果确实蕴含问题 #515。然而,这种联系不是论文的重点,实际上 Erdős 及其上述问题都没有被提及。这种对类似底层概念使用不同词汇是搜索数学文献的常见挑战,使用标准网络搜索很难找到 [LNT84]。

图 II.3:Pommerenke 对问题 #1043 的解决方案,出现在 [Pom61] 的第 7 页
问题 #1043 与其他 15 个问题一起在 [Erd58] 中陈述;其中包括 #1043 在内的几个问题在 [Pom61] 中得到解决。与其他问题不同,问题 #1043 是在两个定理之间的简短附注中处理的,因此被许多人忽略,包括 [Pom61] 的 MathSciNet 评论。此外,事实证明 [Pom59](在 [Pom61] 截图中显示为参考文献 [10])实际上包含了解决问题 #1043 的主要工作,且是用德语写的。GPT-5 为我们翻译并解释了 [Pom59] 中的证明,以便我们自己验证。
II.2.4 展望
部分受我们努力的启发,包括 Thomas Bloom 和 Terence Tao 在内的其他研究人员很快开始在 Erdős 问题网站上发布负面文献搜索,报告 GPT-5 和其他大语言模型无法定位各种问题的现有解决方案。这提供了一个方便的、可众包的"软证书",表明解决方案不太可能出现在已发表的文献中。
数学结果的景观远比任何一位数学家可能掌握的要广泛得多。因此,GPT-5 为执业数学家提供了一种新机制来访问数学文献的集体广度。
II.3 避团码:一个警示故事
以下内容由 Venkatesan Guruswami 和 Parikshit Gopalan 提供,经我们编辑并经他们许可收录
二元线性码是 $\mathbb{F}_2^N \simeq \{0,1\}^N$ 的一个子空间,它避免任何低汉明重量的非零向量。这里我们考虑一个变体,其中码必须避免一组结构化向量,即 $n$ 顶点图中的所有团。这个问题最初来自 [GY14],受最大可恢复码研究的启发,尽管它从未发表过。
让我们正式定义这个问题。设 $[n]=\{1,\dots,n\}$,并用无序对 $\{i,j\}$($1\le i < j\le n$)索引 $\mathbb{F}_2^{\binom{n}{2}}$ 的 $\binom{n}{2}$ 个坐标。对于顶点子集 $S\subseteq[n]$,令 $\chi_S\in \mathbb{F}_2^{\binom{n}{2}}$ 表示 $S$ 上团的边集的指示器,即 $\chi_S(\{i,j\})=\mathbf{1}[i\in S \text{ 且 } j\in S]$。如果对于每个 $|S|\ge 2$ 的 $S\subseteq[n]$ 有 $\chi_S\notin C$,则二元线性码 $C\subseteq \mathbb{F}_2^{\binom{n}{2}}$ 是避团的。
向 GPT-5 提出的问题如下:
作为顶点数 $n$ 的函数,避团码的最小奇偶校验数(即最小余维数)$r = r(n)$ 是多少?
一个简单的概率(随机编码)论证给出以下上界,GPT-5 也立即找到了(有一些加性 $O(1)$ 松弛):
我们有 $r(n) \le n$。
人们很容易认为随机编码界是紧的,但没有明显的下界。这是我们向 GPT-5 提出的问题(实际上我们自己没有认真思考过)。最初,它确信这个界是紧的(相差一个加性常数),并试图用一系列有错误的论证来说服我们,诉诸线性代数和权威证明:
- 最有趣的是一个幻觉回应,大意是我们中的一个人曾在 TCS Stack Exchange 上问过这个问题,给他们的答案是 $n$。这两个说法都是不正确的。
- 另一个不正确的论证仍然包含主要想法的萌芽。它是考虑二次形式 $Q_1,\ldots, Q_r$,然后查看校验子 $S(x) = (Q_1(x), \ldots, Q_r(x))$ 并声称 $x \mapsto S(x)$ 是单射,因此 $r \geq n$。这个声明也是错误的。
- 当被质疑时,GPT-5 提出了一个基于经典 Chevalley-Warning 定理的优雅(且正确的)代数论证,建立了下面的定理 II.3.2。
对于所有 $n \ge 2$,$r(n) \geq \lfloor n/2\rfloor$。
我们后来发现了一个构造(没有使用 GPT-5)表明下界是恰好紧的:上面的简单概率界是次优的,实际上对所有 $n$ 有 $r(n)=\lfloor n/2\rfloor$。
II.3.1 意外的转折
我们非常兴奋能够得到一个我们好奇多年的问题的精确解,特别是因为证明的一个方向是由 AI 完成的。然而,我们很快得知,相同的紧界(以及匹配上界的不同证明)几乎 3 年前就出现在 Arxiv 上的短论文 [Alo22] 中。事实上,GPT-5 的下界证明与 Alon 的完全相同!因此,GPT-5 似乎重现了 Alon 的证明并在没有意识到其来源的情况下传递给我们。事实证明,对 GPT-5 Pro 的新尝试能够恢复这个来源,如图 II.4 所示。
你知道关于以下问题的任何信息吗?这涉及一个二元线性码 $C \subset \mathbb{F}_2^{\binom{n}{2}}$ 的最小余维数,该码避免所有团的指示器(当码字位置自然地被视为 $n$ 个顶点的完全图的边时)。
答案。是的。不包含任何团指示器的二元线性码 $C \subset \mathbb{F}_2^{\binom{n}{2}}$ 的最小可能余维数恰好是
解释(概要)。
余维数为 $r$ 的线性码是 $r$ 个奇偶校验的公共核。等价地,我们选择 $[n]$ 上的图 $G_1,\dots,G_r$,向量 $x \in \mathbb{F}_2^{\binom{n}{2}}$ 在 $C$ 中当且仅当 $\langle x, 1_{E(G_i)} \rangle = 0$ 对所有 $i$ 成立。避免所有团指示器意味着对于每个非空顶点集 $T \subseteq [n]$,团 $K_T$ 满足 $|E(K_T) \cap E(G_i)| \equiv 1 \pmod{2}$ 对至少一个 $i$ 成立。
结论。两个界匹配,因此精确的最小余维数是 $\lfloor n/2 \rfloor$。完整、优雅的展示请参见 N. Alon,Graph-Codes,定理 1.6。
我们的经历说明了使用 AI 的一个陷阱:尽管 GPT-5 拥有巨大的内部知识以及使用互联网定位更多知识的能力,但它可能并不总是准确报告原始信息来源。这有可能欺骗即使是经验丰富的研究人员,让他们认为自己的发现是新颖的。我们预计我们的经历并非独特,并敦促其他人在使用 LLM 辅助证明时特别注意归因。
III. 与 AI 协同工作
III.1 使用 LLM 作为研究伙伴的近期经验 — Timothy Gowers
这是一份关于在实际进行数学研究时使用 LLM 的一两次近期经验的简要报告,所谓实际研究是指在早期阶段思考研究级问题,我有一些想法但尚未找到看起来可能有效的方法。到目前为止,我可以这样总结情况:我还没有(尚未)经历过 LLM 做出决定性贡献的情况,但我发现它们在以下方面很有用:
- 如果我怀疑我提出的定义或数学观察已经存在于文献中,LLM 通常可以帮助我找到它。GPT-5 在这方面似乎明显优于 GPT-4。特别是,根据我使用 GPT-5 的经验,参考文献很少是幻觉,即使是幻觉也可能指向实际存在且有用的参考文献。
- 我有时会提出一些定义明确的子问题,看起来不会太难但也看起来需要一些时间来解决,而 GPT-5 可以在几秒钟内为我解决它们。
- 我有一些相当精确的解决问题的想法,我把它们提交给 GPT-5 Pro,它向我解释了为什么这些想法行不通。
在消极方面,如果我问更开放式的问题,或者提供更粗略的证明尝试想法,那似乎会鼓励 LLM 更令人烦恼的特性显现出来:它们会告诉我我的想法确实有效,并写出一些据称能充实细节的东西,但经不起仔细审查。这甚至适用于 GPT-5 Pro,我在撰写本文时已经使用了几天。
综合考虑这些,我目前对 LLM 的评估是:它们刚刚开始作为研究合作者变得有用:人们可以像与人类合作者那样与它们交流想法,并且可以非常快速地得到回应。就像人类合作者一样,即使是 LLM 不太好的想法有时也能激励我取得进展。(我把这称为"这显然行不通……但等等!"现象。)所以我们已经到达了这样一个阶段:LLM 可以加速思考问题的过程,特别是如果这个问题稍微超出了自己的主要专业领域,但我们还没有达到 LLM 可能拥有解决困难问题的主要想法的阶段。(最后这句话需要仔细解读。我可能发现一个问题困难是因为我不熟悉解决它所需的领域特定技巧,但如果这个问题对于具有相关专业知识的人来说会很容易,那么对 LLM 来说也可能很容易。因此,所谓"困难"是指一个问题,相关领域的标准技巧工具箱不足以解决。)
我将在这里给出两个与 GPT-5 和 GPT-5 Pro 最近交互的例子。我强调,在每种情况下,LLM 的主要贡献是为我节省了少量时间:它所做的观察和提供的证明是我期望自己在不太长的时间内找到的,但在 LLM 的帮助下,我根本不需要做任何努力,几秒钟内就得到了答案。
有趣的是,思考一下我是否应该在求助 LLM 之前付出更多努力。每个人都必须自己做出这个决定。我目前的感觉是,这个问题有点像是否应该使用计算器来做算术的问题。如果你知道如何自己进行计算,只把计算器作为节省时间的工具,你显然是更好的计算器用户。同样,在这些早期阶段,如果我认为 LLM 正在执行我对如何处理有很好的想法、并且在给定一点时间的情况下几乎肯定可以不借助帮助完成的任务,我会更舒服地请求 LLM 帮助。我不太愿意简单地给它一个困难问题并希望得到答案(而且,目前,如果我这样做也不太有信心会得到有用的答案)。
例 1:$L_2$ 的紧子集
我试图解决一个问题,其中我有一个相当复杂的非线性映射 $T:L_2\to L_2$,我想证明某个函数 $f$ 的迭代 $f, Tf, T^2f,\dots$ 收敛。根据我对 $T$ 的了解,证明迭代有收敛子序列显然就足够了,所以我在寻找一个紧子集 $K\subset L_2$,我可以论证它包含所有迭代。
我知道在任意 Banach 空间中,紧集的一个来源是零序列的凸包,经过一番思考后,我意识到我可以证明在 $\ell_2$ 中,如果我取任何非负平方可和序列 $s$,那么集合 $\{a\in\ell_2:|a|\leq s\}$ 是紧的。我有理由相信 $f$ 的迭代会表现出类似高斯衰减的特性,所以我想知道被高斯函数上界的函数集合是否有类似的结果。
我很快意识到情况不可能如此,因为可以取一系列越来越快速振荡的函数,它们将没有收敛子序列。
然而,我有理由相信 $f$ 在映射 $T$ 下的迭代不会开始越来越振荡,所以我没有失去希望。我想到振荡应该在傅里叶变换侧显现出来,由于操作 $T$ 与傅里叶变换交互良好,如果 $f$ 和 $\hat f$ 都被高斯函数上界的函数集合是紧的,这可能就足够了。
这对我来说似乎是合理的,所以我向 GPT-5 询问了这个问题。22 秒后,它给我提供了一个证明,该证明依赖于一个我没听说过的引理,叫做 Kolmogorov-Riesz 引理。给定这个引理,证明看起来是正确的,而且引理看起来是合理的。我在网上查了一下,发现它确实存在。我不知道我自己需要多长时间才能意识到这个引理是正确的中间步骤(之后我可以使用 GPT-5 的语义搜索功能),但我估计这为我节省了一到三个小时的工作。
这个故事有一个后记。我正在与两个研究生合作这个项目,他们也很擅长指出我证明方法建议的缺陷。特别是,其中一人指出,$f$ 和 $\hat f$ 都被标准高斯函数上界的条件会太强,因为 Hardy 不确定性原理意味着在这种情况下 $f$ 本身必须是标准高斯函数的倍数。感谢这个评论,我意识到我认为可以获得的条件——$f$ 和 $\hat f$ 都被某个高斯函数 $e^{-cx^2}$ 上界,但不一定 $c=1/2$——与我问 GPT-5 的条件不匹配。所以我然后问 GPT-5 在这个更弱的假设下是否仍然有紧性。同样,它很快告诉我答案,这种情况下的答案是我自己会相当快意识到的,但没有 GPT-5 快。不幸的是,答案是否定的:Hermite 函数(傅里叶变换的特征函数)形成一个满足条件但没有收敛子序列的序列。
我被这个骗了,因为每个 Hermite 函数是一个多项式乘以 $e^{-x^2/2}$,因此如果 $c < 1/2$ 则衰减比 $e^{-cx^2}$ 更快。然而,在写上一段时,我开始有些怀疑,因为我追求的是一系列都被某个固定的 $Ce^{-cx^2}$(某个固定的 $C$ 和 $c$)所控制的函数,虽然每个 Hermite 函数当 $c < 1/2$ 时最终被 $e^{-cx^2}$ 控制,但这是一个更弱的陈述。既然我现在可以问 GPT-5 Pro,我问是否可能存在一个形如 $Ce^{-cx^2}$($c>0$)的单一函数控制所有 Hermite 函数。它告诉我答案是否定的,并给出了以下令人信服的证明。Hermite 函数满足递归关系
$$xh_n=\sqrt{\frac{n+1}{2}}h_{n+1}+\sqrt{\frac{n}{2}}h_{n-1}.$$
由于 Hermite 函数是正交归一的,所以
$$\int_{-\infty}^\infty x^2h_n(x)^2\,dx=\frac{n+1}{2}+\frac{n}{2}=n+\frac{1}{2}.$$
因此,对于足够大的 $n$,它至少是 $C^2\int x^2 e^{-cx^2}\,dx$(因为后者是有限的且与 $n$ 无关),这证明了对于足够大的 $n$,$|h_n|$ 不能被 $Ce^{-cx^2}$ 控制。
我然后问 GPT-5 Pro,如果 $0 < c < 1/2$,使得 $|f|$ 和 $|\hat f|$ 被 $Ce^{-cx^2}$ 控制的函数 $f$ 的集合是否是紧的。它告诉我答案是肯定的,并给出了一个看起来令人信服的证明,但我觉得需要检查,特别是它说推导的某个步骤来自 Hardy 不确定性原理的"半群版本",但没有给出该版本实际说了什么的细节。当我要求更多细节时,它给了我一个幻觉的参考文献,但作者写过密切相关的主题。我抱怨说找不到那篇论文,这次它给了我一个高度相关的论文的参考文献,虽然作者名字写错了。除非我犯了另一个错误,这篇论文恰好包含我想要的结果:在给定条件下,它给出了 $f$ 的 Hermite 系数的上界,这个上界以指数速率衰减。因此,存在一个零序列,其凸包包含所有这样的函数 $f$,给我们所需的紧性。
故事的最后转折是我的人类合作者的另一个评论。我在假设所有使得 $|f|$ 和 $|\hat f|$ 被 $Ce^{-cx^2}$ 上界的 $f$ 的集合在 $T$ 下不变时有点粗心,所以我们现在拥有的紧性结果并不明显足以满足我们的目的。尽管如此,我们在思考这个问题上已经取得了重大进展,与 GPT-5 和 GPT-5 Pro 的来回对话大大加速了这个过程。
例 2:具有异常小团数的图
我最近听说了一个非常好的问题,它问是否存在一个具有以下性质的算法:
- 它以具有 $n$ 个顶点的图作为输入。
- 如果图不包含大小为 $(3/2)\log_2 n$ 的团,则输出 1。
- 对于几乎所有图(意味着 $1-o(1)$ 的比例,但即使是 99% 也很有趣),它输出 0。
- 它在多项式时间内运行。
人们可能希望存在这样一个算法的原因是,随机图以高概率具有大约 $2\log_2 n$ 的团数,并且通常会有许多大小为 $(3/2)\log_2 n$ 的团,这些团将高度分散,所以消除所有这些团似乎很困难。因此,人们期望没有大小为 $(3/2)\log_2 n$ 的团的图必须具有某种"意外结构",可以被有效算法捕获。(相比之下,添加一个意外大的团是很容易实现的:只需随机添加它。如果这种"植入团"的大小小于 $\sqrt{n}/\log n$,则似乎很难找到。)
我决定尝试想办法创建一类没有大小为 $(3/2)\log_2 n$ 的团,但看起来是随机的因此难以有效检测的图。我的每一个想法,GPT-5 Pro 都能在几秒钟内推翻(总是先告诉我它喜欢这个想法来软化打击)。
第一个想法:使用线性代数
组合学中一个著名的结果,当你第一次看到时很惊讶,是如果所有交集都是偶数大小,那么你可以拥有的 $\{1,2,\dots,n\}$ 的奇数大小子集的数量是 $n$。证明只有一行:以通常的方式将每个子集解释为 01 序列,并将序列视为 $\mathbb{F}_2^n$ 中的向量。两个集合的交集的奇偶性变成两个对应向量的 $\mathbb{F}_2$ 内积,而线性独立向量序列的通常证明可以很容易地改编为证明奇数大小和偶数交集的集合对应于线性独立向量,因此最多有 $n$ 个。
如果我们形成一个图,其中顶点是所有奇数大小的集合,如果它们的交集有偶数大小则两个顶点由边相连,那么上述结果告诉我们不可能有大于 $n$ 的团。由于有 $N=2^{n-1}$ 个顶点,这个图没有大小为 $(3/2)\log_2 N$ 的团(对于足够大的 $N$)。
到目前为止,它很容易与随机图区分:例如,它比典型的随机图要规则得多。我提议通过传递到大小为 $2^{\alpha n}$(某个相当接近 1 的 $\alpha$)的随机顶点子集来解决这个问题。
GPT-5 Pro 指出,这样一个矩阵在 $\mathbb{F}_2$ 上的秩最多是 $n$,而 $2^{\alpha n}$ 个顶点上随机图的邻接矩阵的秩通常接近 $2^{\alpha n}$,所以有一个非常简单的算法来挑出我提出的这类矩阵。
第二个想法:使用单位向量之间的角度
我的第一个想法失败了,因为它在某种意义上太代数化了,但我想到我知道另一个关于向量的结果,它暗示了没有大团的图的存在。它指出,你可以在 $\mathbb{R}^d$ 中找到的使得任何两个向量内积为负的最大向量数量是 $d+1$(以原点为中心的正则单纯形的顶点达到等式)。所以我想知道以这样的方式选择 $d$ 使得 $d+1 < (3/2)\log_2 n$,然后在 $\mathbb{R}^d$ 中选择 $n$ 个随机单位向量 $u_1,\dots,u_n$,当且仅当它们有负内积时用边连接它们中的两个。这让我感觉有可能有效,因为虽然元素为 $\langle u_i,u_j\rangle$ 的矩阵(以概率 1)秩为 $d$,但我们对每个矩阵元素应用了相当剧烈且非代数的操作:如果是负的就替换为 1,否则替换为 0。
然而,GPT-5 Pro 几乎立即给了我一个检测用这种方法创建的矩阵的测试,基于 $\langle u_i,u_j\rangle$ 越大,随机向量与它们两个都有正内积的可能性就越大这一事实。事实上,如果 $u_i$ 和 $u_j$ 形成角度 $\theta$,这个概率是 $1/2-\theta/2\pi$。从简单计算可得,在任何用我提出的方法获得的图中,大小为 3 的独立集会比随机图中预期的明显更多,也会有许多邻域交集比预期大得多的顶点对。
我然后注意到这种形式的测试也适用于 $\mathbb{F}_2^n$ 构造,因为如果 $x+y+z+w=0$,那么任何与 $x,y$ 和 $z$ 相连的顶点 $v$ 自动与 $w$ 相连。传递到大小为 $2^{\alpha n}$($\alpha$ 相当接近 1)的子集会留下许多加起来为 0 的四元组 $x,y,z,w$,它们的邻域交集会大得多。
第三个想法:用多项式替换线性代数
我相当模糊地想知道是否可以通过设计某种多项式条件来使 $\mathbb{F}_2^n$ 的两个元素 $x,y$ 相连来挽救更代数化的方法。也就是说,也许我可以找到某个合适的多项式映射 $P:\mathbb{F}_2^n\times\mathbb{F}_2^n\to\mathbb{F}_2$(关于 $x$ 和 $y$ 对称),当且仅当 $P(x,y)=1$ 时在 $x$ 和 $y$ 之间放一条边。
这次 GPT-5 Pro 给了我一个较长的答案,解释说除非 $P$ 的度数很大,否则得到的矩阵仍然会有低秩。这似乎是可信的,但我没有仔细检查论证。再次问 GPT-5 Pro 同样的问题(只是关于这样一个矩阵的秩),我得到以下简单论证:这个我自己可能需要几分钟才能找到,所以再次有加速但没有其他一些问题那么多。设 $P$ 的度数最多为 $d$。如果我们考虑矩阵的第 $x$ 行,那么它的值是 $P(x,y)$,其中 $y$ 遍历 $\mathbb{F}_2^n$。对于固定的 $x$,$P(x,y)$ 是关于 $y$ 的度数最多为 $d$ 的多项式,所以它被单项式 $x_{i_1}\dots x_{i_s}$($s\leq d$)张成,因此当我们将它们视为从 $\mathbb{F}_2^n$ 到 $\mathbb{F}_2$ 的函数时,该行被这些单项式张成。特别是,行空间的维数最多为 $\sum_{s=0}^d\binom{n}{s}$。要使这个不明显小于 $2^{\alpha n}$(我想象我也传递到了大小为 $2^{\alpha n}$ 的随机顶点子集),我们需要 $d$ 与 $n$ 成线性关系。
但 GPT-5 Pro 也告诉我,如果 $P$ 的度数那么大,图中就没有明显的理由不包含大小为 $(3/2)\log_2 N$ 的团,其中 $N$ 是顶点数。如果我没记错,它没有给出特别令人信服的论证,但它与我的直觉一致,以至于我认为不需要详细辩护这个断言。
尝试反方向
鉴于我对前两个尝试例子的失败有一个统一的解释,我然后决定讨论是否可以证明通过某些基于邻域交集大小的强随机性测试的图包含大小为 $(3/2)\log_2(n)$ 的团。我收到的答案没有帮助,这并不奇怪,因为我的问题太开放了,关于给出大小高达 $(3/2)\log_2 n$ 的子图计数信息的拟随机性条件,似乎知之甚少。
结论
作为研究导师,我有一个经验法则来判断我对博士生研究的贡献何时达到应该成为共同作者的水平。规则是,如果学生来与我讨论问题,而我在讨论过程中有一个对我来说比对他们更自然的想法,并且这个想法最终是有帮助的,那么这还不足以成为共同作者。但如果我花时间努力解决这个问题(当然,只有当项目正式是合作项目时我才会这样做),并且在努力过程中我提出了一个不仅仅是我恰好拥有的标准专业知识的想法,那么我就对工作做出了真正的贡献。
到目前为止,我使用 LLM 的经验是,它们能够与我一起扮演这种知识渊博的研究导师角色,考虑到它们拥有多少知识,这可能非常有用,但它们还没有达到(或者至少在我自己与它们的互动中还没有表现出)一个遵循我上述惯例的人类数学家会要求共同作者身份的水平。
III.2 宇宙弦引力辐射的功率谱 — Robert Scherrer
问题背景
宇宙弦是假设的一维拓扑缺陷,可能在早期宇宙的宇宙学相变中形成(参见例如 Hindmarsh 1995 年的综述)。在 1980 年代经历了一阵兴趣高潮后,对宇宙弦的兴趣急剧下降。然而,最近对这些对象的兴趣重新复苏,因为它们可以作为脉冲星计时阵列最近观测到的随机背景等引力辐射的丰富发射源。
在之前的一篇论文中,我的研究生(David Storm)和我研究了 Garfinkle 和 Vachaspati 首先研究的一类宇宙弦可能产生的辐射谱。虽然这些宇宙弦引力辐射的每单位立体角总功率在 Garfinkle 和 Vachaspati 的论文中已经研究过,但与随机背景相关的量是作为第 $n$ 次谐波函数的总功率 $P_n$。具有单位长度质量 $\mu$ 的宇宙弦在单位向量 $\hat r$ 方向上以频率 $\omega_n = 4\pi n/L$(其中 $L$ 是环的长度)发射的功率由下式给出:
$$P_n = \frac{32 G\mu^2}{\pi^3 n^2} \int d\Omega \frac{[1- (-1)^n \cos(n \pi e_1)][1- (-1)^n \cos(n \pi e_2)]}{(1-e_1^2)(1-e_2^2)},$$
其中 $e_1 = \hat r \cdot \hat{a}$ 和 $e_2 = \hat r \cdot \hat{b}$,$\hat{a}$ 和 $\hat{b}$ 是表征弦轨迹方向的单位向量。由于 $\hat{a}$ 和 $\hat{b}$ 是三维单位向量,问题完全由 $\hat{a}$ 和 $\hat{b}$ 之间的角度 $\alpha$ 表征。方形环有 $\alpha = \pi/2$,而较小的 $\alpha$ 值对应于更扁长的矩形环。
在我们早期的论文中,我们检验了一系列 $\alpha$ 值,并在数值上发现 $dP_n/d\Omega$ 在大 $n$ 时没有按照先前论证的 $n^{-2}$ 缩放,而是似乎偏离了预测结果。由于我们的结果与公认的观点不一致,因此解析地确认它们很重要。
人类路线。在大约六个月的攻关后,我能够推导出部分结果,但仅适用于最简单的情况:$\alpha = \pi/2$。此外,我的结果只适用于偶数 $n$。在这种情况下,我发现
$$P_n = \left[ \frac{128 G\mu^2}{\pi^2 n^2}\right ] \left[\gamma + \ln \pi + \ln(n)\right],$$
其中 $\gamma$ 是欧拉常数。推导的细节可以在 Storm 和 Scherrer 论文的附录中找到。
交给 GPT-5 Pro 的任务:目标、提示词和模型行为
目标。虽然我最终的目标是解析地确定所有 $\alpha$ 的功率谱,但作为第一步,我请求 GPT-5 Pro 为奇数 $n$ 值推导 $P_n$——或者更确切地说,是上式中出现的积分。我从数值结果中知道,在大 $n$ 极限下,它几乎肯定与上述公式具有相同的形式,但我用来推导这个结果的方法不能应用于奇数 $n$ 的情况。
提示词。在我的初始提示词中,我请求 GPT-5 Pro 对奇数 $n$ 评估上式中的积分,并给出大 $n$ 的渐近行为。程序卡住了相当长的时间,没有给我任何关于其思考过程的细节。几个小时后我变得沮丧并杀掉了它。然后我重复了提示词,但添加了对 Storm 和 Scherrer 论文的引用。确切的提示词是:
我想在球面上解析地积分以下积分,所以在球坐标中 theta 从 0 到 $\pi$,phi 从 0 到 $2\pi$。积分是 $[1+ \cos (n \pi e_1)][1+ \cos(n \pi e_2)]/[(1 - e_1^2)(1-e_2^2)]$ 的积分,其中 $n$ 是奇整数,$e_1 = \cos(\theta)$ 和 $e_2 = \sin(\theta) \sin(\phi)$,其中 $\theta$ 和 $\phi$ 是球坐标中的通常坐标:$\theta$ 是相对于 $z$ 轴的角度,$\phi$ 是方位角。我想要所有奇数 $n$ 的精确解,但如果你不能解决一般情况,你可以假设 $n$ 比 1 大得多。注意,Scherrer 和 Storm 在他们发表在 Physical Review D 上的论文中推导了偶数 $n$ 的解。
我对 $\theta$ 和 $\phi$ 的定义特别啰嗦,因为在球坐标中,物理学家使用与数学家相反的惯例,我不确定 GPT-5 Pro 会默认使用哪种惯例。我还在原式中取 $n$ 为奇数并去掉了 $(-1)^n$ 因子。
结果。在推理了 40 分钟后,GPT-5 Pro 为大奇数 $n$ 产生了一个与我之前为大偶数 $n$ 推导的渐近结果相同的结果。它使用了一种与我完全不同的解法。虽然我自己的解法涉及将积分分成三部分并对每部分采取临时方法,但 GPT-5 使用了勒让德多项式展开,然后将其扩展为贝塞尔函数展开。我怀疑某种贝塞尔函数解法是可能的,但从未自己找到。GPT-5 Pro 还给出了这个公式的前导修正项,使其变为
$$4 \pi [\ln(n\pi) + \gamma - \text{Ci}(n \pi)],$$
其中 Ci 是余弦积分函数。我不知道这个修正项,它对小 $n$ 值相关。此外,GPT-5 Pro 提供了一个表格,说明数值积分与大 $n$ 渐近结果的比较,显示它们在小 $n$(小于 5)时彼此偏离,但在大 $n$ 时几乎相同。(我应该提到,即使数值积分也很困难——角坐标中的被积函数如此尖锐,以至于它像海胆一样)。GPT-5 Pro 还断言(正确地)提示词中的积分对偶数 $n$ 不收敛,但这是因为我省略了原式中的 $(-1)^n$ 因子。
作为参考,完整的交互可在此处获得:ScherrerGPT。
结果、影响和下一步
结果。GPT-5 Pro 推导了一个新的解析结果,确认了我们早期对一类宇宙弦引力波功率谱的数值模拟。如果我早点获得这个结果,我会将其纳入我们的论文。
影响。GPT-5 Pro 能够解决超出 Mathematica 等符号操作程序能力的复杂解析积分。
下一步。明显的下一步将是解决任意 $\alpha$ 的一般情况。如果成功,这将提供一个足够重要的结果来激励研究出版。我积累了许多这样的未解决的有趣数学问题,这些问题在我 40 年的研究生涯中让我感到沮丧。其中许多似乎特别适合 AI 解决。我期待这一时刻已经很久了。
III.3 AI 辅助热核燃烧传播的简化物理建模 — Brian Keith Spears
前提
GPT-5 已经发展成为一个相当有能力的研究助手。它现在的显著之处在于其中等深度的知识(相对于,比如说,一个有 20 年经验的博士研究员)横跨了令人难以置信的广泛主题。我们在这里通过招募它的帮助来制定一个惯性约束聚变问题来测试和利用这一能力,该问题探索了这种广度。
我们的目标是改进对聚变点火和燃烧传播在热核燃料冷热界面处的局部物理的理解——这是一个关键的复杂过程,导致聚变产生的能量超过 ICF 靶吸收的能量。为此,我们建立了一个简化物理模型,将热核燃烧波的产生与完整 ICF 内爆模拟的复杂内爆动力学隔离开来。
我们对几个问题阶段的 AI 驱动辅助感兴趣:
- 建立一个简化的物理模型,用以发展直觉;
- 这种模型的数值模拟和求解;
- 设计数值实验来帮助我们引出关键的物理敏感性;
- 发展一个解释数值发现的理论。
我们开发了一个简化的、静态的(无流体运动)反应-扩散模型,用于 ICF 氘-氚(DT)靶,以研究热核燃烧波向冷、密燃料的点火和传播。这个框架平衡了保真度和透明度:它隔离了热传导、α 粒子能量沉积、辐射损失和密度轮廓整形对波传播的相对作用。
引言
为了开始,我提示 GPT-5 帮助我建立一个模型环境,我可以用它来探索惯性约束聚变(ICF)中的热核燃烧传播。这种物理将复杂的微观物理与陡峭的热力学梯度耦合,我想故意去除不断且关键地改变功率平衡的动力学。目标只是在静态情况下找到理想的聚变界面;稍后我们可以弄清楚如何将其映射到真实的内爆中并控制它(通过激波时序、驱动预热等)。
我以通常的方式开始,用一个可能(也许不是亲切地)被称为"老派提示词"的东西:
我想探索热核燃烧波传播到内爆 ICF 靶中冷氘-氚燃料的动力学。我想在球形几何中构建一个简化的、静态的(无材料运动)模型来模拟这种波的点火和传播。
让我们构建一个反应扩散方程来模拟它。我希望模型有 3 个区域。第一个区域是热的、低密度的 DT 等离子体(热斑),它将启动燃烧波。它应该具有类似于 NIF 内爆在峰值离子温度时中心热斑的性质,并且应该具有类似的半径。下一个区域将是相对冷的、致密的 DT 燃料,具有二次密度轮廓(一个平均斜率参数和一个曲率参数),从热斑的密度上升到高密度冷燃料,以及从热到冷的类似温度上升。第三个也是最后一个区域是均匀密度的(相对)冷燃料,也在 NIF 内爆在峰值壳层压缩时(反弹激波通过后)良好激波时序的条件和厚度下。
反应扩散方程动力学应该清楚地捕获三个效应:首先,热能应该根据密度和温度相关热扩散率的良好近似进行扩散;其次,反应项应该捕获 α 粒子产生的能量生成以及该 α 能量与附近材料中条件相关阻止本领一致的非局域沉积;最后,应该有辐射损失,它被传输到远离局部热前沿的地方。
有了这个模型,我们想问一个关键问题。区域 2 中什么密度轮廓最容易让我们传播燃烧波?我们推测,对于非常浅的斜坡,热斑最初可以轻松加热区域二,但波传播"熄灭"。对于非常陡的斜坡,我们推测需要热斑中更多的能量来启动波,但它传播得更容易。因此,直觉是存在一个最优轮廓(平均斜率和曲率)。
用适当的物理常数和假设建立这个模型。将其嵌入一个优化框架中,该框架提供最稳健的燃烧波启动和传播的轮廓斜率。用几张图展示在几种情况下的温度波传播结果,并添加一个品质因数图,横轴为燃料轮廓(斜率和曲率),纵轴为传播深度(或速度)差异。
这个初始提示词导致了与 GPT-5 Pro 的长时间对话,有很多来回交流,我在这里省略了。本节的其余部分总结了我与 GPT-5 Pro 合作能够进行的工作。这里给出的大部分结果都是由 GPT-5 产生的;我只是提供了一些反馈和指导。有兴趣的读者可以参阅这里与 GPT-5 Pro 的长时间交流。
模型公式
结果是一个相当好的静态模型开端——公式是好的,项被恰当地形成和命名,物理性质选择是相关的。经过一些对话,我们确定了熟悉且更详细的物理数据,所有这些都是在我请求之前由 GPT-5 提供的。这就是与国家实验室同事和专家的对话方式。
我们一起考虑无材料运动的球对称。因变量是局部 DT 温度 $T(r,t)$,单位为 keV。DT 等离子体的能量守恒(忽略 $PdV$ 功)表示为
$$\rho C_v \frac{\partial T}{\partial t} = \frac{1}{r^2} \frac{\partial}{\partial r}\left( r^2 \rho \,\chi(T,\rho)\,\frac{\partial T}{\partial r} \right) + Q_\alpha(T,\rho) - Q_{\text{rad}}(T,\rho),$$
其中 $C_v = \frac{3}{2}k_B/m_i$ 是单位质量的比热,$\chi$ 是热扩散率,$Q_\alpha$ 是 α 粒子加热源,$Q_{\text{rad}}$ 是体积辐射损失。
对于热输运,我们采用电子热传导的 Spitzer-Härm 标度律:
$$\chi(T,\rho) = \chi_0 \frac{T^{5/2}}{\rho},$$
其中 $\chi_0=0.12$ 选择来近似 5-10 keV 和 $\rho \approx 1\,\text{g cm}^{-3}$ 附近磁化 DT 等离子体的扩散率。(磁化值的选择是有争议的,且不保守,但我们将让它在我们的实验中滑过。)
聚变功率密度遵循 DT 反应性 $\langle \sigma v\rangle$ 的 Bosch-Hale 拟合:
$$P_{\text{fus}} = n_D n_T \langle \sigma v\rangle E_{\text{fus}},\quad E_{\text{fus}} = 17.6\,\text{MeV},$$
其中 $n_D = n_T = \rho/(2m_i)$。α 粒子加热源是
$$Q_\alpha = f_\alpha P_{\text{fus}},$$
其中 $f_\alpha = E_\alpha/E_{\text{fus}} = 3.5/17.6 \approx 0.199$。
我们使用非局域 Helmholtz 算子模拟有限射程 α 输运:
$$\left( I - \lambda_\alpha^2\nabla^2 \right) q_\alpha = f_{\text{dep}} P_\alpha,$$
其中 $\lambda_\alpha(T,\rho) = R_m(T)/\rho$,$R_m(T)$ 是 α 质量射程(单位 g cm$^{-2}$)。采用的物理上现实的表是
$$R_m(T) = 0.30\left(\frac{T}{3\,\text{keV}}\right)^{1/2}\,\text{g cm}^{-2},$$
与 3.5 MeV α 阻止数据一致。沉积被限制在总能量的 90%($f_{\text{dep}}\le 0.9$)以模拟逃逸。
最后,对于辐射损失,我们使用带逃逸概率的近似灰色扩散:
$$Q_{\text{rad}} = C_{\text{rad}}\,\rho^2\sqrt{T}\,\frac{1}{1+\kappa_0\rho R_{\text{out}}},$$
其中 $C_{\text{rad}}=3\times10^{-36}\,\text{W m}^3\text{ kg}^{-2}\text{ keV}^{-1/2}$,$\kappa_0=5\times10^{-3}$ 近似 DT 的 Rosseland 平均不透明度。
GPT-5 非常擅长这种模型开发和设置。它需要我很少的干预就能使这个模型可信和完整。这在数值部分会改变。
数值实现
GPT-5 在没有明确提示的情况下,为偏微分方程(PDE)选择了在均匀径向网格($N\approx150$ 个点)上求解的二阶 Crank-Nicolson 隐式格式。时间积分使用自适应子步进行,最长 10 ns。边界条件:
$$\frac{\partial T}{\partial r}=0 \quad \text{at } r=0, \qquad \frac{\partial T}{\partial r}=0 \quad \text{at } r=R_{\text{outer}}.$$
反应、扩散和辐射源项通过算子分裂分离。α 沉积通过每步三对角 Helmholtz 反演求解。
这些对于我们寻求开发的测试平台来说是合理的选择。应该注意的是,这花了几分钟就编码完成了。虽然我可以做到这一点,但我不是每天都做,我怀疑我需要几个工作日才能真正得到可靠的代码工作。关键是,我现在可以在几分钟内交付,就好像我处于我在这种工作上最高水平一样。会有人说这个实现并不出色,确实不是。但是,几分钟内完成是出色的。
正是在这一点上,我的人类劳动和智慧是必需的。我需要为聚变边界的密度和温度轮廓提出一些参数化建议。GPT-5 还需要我帮助它找到展示我们正在寻找的那种阈值行为的参数空间区域。使热斑太强,整个系统会奇异地爆炸。使它太弱,不会有燃烧波启动和传播。要理解我们想象的轮廓的效果,我们需要一个微妙平衡的边际系统。鉴于 ICF 的非线性,这不仅需要直觉,还需要一些数值经验主义。GPT-5 让我在这里工作。
对于密度轮廓,指定了三个区域:
- 区域 1(热斑):$r \le R_{hs}$,$\rho = \rho_{hs} \approx 1.2\,\text{g cm}^{-3}$。
- 区域 2(斜坡):$R_{hs} < r \le R_{hs}+L_{\text{ramp}}$, $$\rho(r) = \rho_{hs} + s(r-R_{hs}) + c(r-R_{hs})^2,$$ 缩放以确保 $\rho(R_{hs}+L_{\text{ramp}})=\rho_{\text{cold}}$。
- 区域 3(冷燃料):$\rho = \rho_{\text{cold}} \approx 150\,\text{g cm}^{-3}$。
斜坡由斜率 $s$ 和曲率 $c$ 控制,范围为
$$s \in [1.5,6.5]\times10^9\,\text{kg m}^{-4} \quad\text{和}\quad c \in [-6.5,0]\times10^{13}\,\text{kg m}^{-5}.$$
我花了几个小时调整热斑条件、冷燃料条件、电导率、α 粒子阻止本领和轮廓设计,以获得物理上合理的结果。这种活动是我们 ICF 界可能称之为"设计工作"——达到物理有趣和有用的地方。GPT-5 是一个糟糕的设计师,提供的结果是空的、嘈杂的或无效的(NaN),同时声称已经取得了荣耀。然而,当重新提示检查病态结果或空信号时,GPT-5 提供了相当复杂的解决方案,包括不同的 FFT 实现以防止混叠、改进的分辨率以跟踪燃烧前沿、改变的性能指标以放大信号。如果用户在第一个古怪的回应时放弃,他们会错过模型相当强大的能力。必须强调的是,这需要你是一个非常自信的物理学家。你必须知道断言是错误的,你必须自信地推动更好的解决方案,你必须足够好以知道何时达到了真正的解决方案。我经常发现 GPT-5 提供的解决方案,我必须深入思考才能确定它们是否实际上是正确的,还是只是方便的。
我们在固定热斑温度 $T_{hs}=1.5\,\text{keV}$ 下进行了模拟。对于每个(斜率,曲率)对,通过最小二乘拟合测量 1-3 ns 之间 5 keV 等温线的平均前沿速度:
$$v_{\text{mean}} = \frac{\displaystyle\int_{t_0}^{t_1} \frac{dr_f}{dt}\,dt}{t_1-t_0}.$$
得到的 $v_{\text{mean}}(s,c)$ 场用高斯核(10% 带宽)平滑以去除插值噪声。40-100 km s$^{-1}$ 的等高线清楚地揭示了一个传播脊,中心位于大约
$$s^{*} \approx 3.0\times10^9\,\text{kg m}^{-4}, \qquad c^{*} \approx -4.5\times10^{13}\,\text{kg m}^{-5},$$
局部最大值高达 $v_{\text{mean}}\approx 100\,\text{km s}^{-1}$。
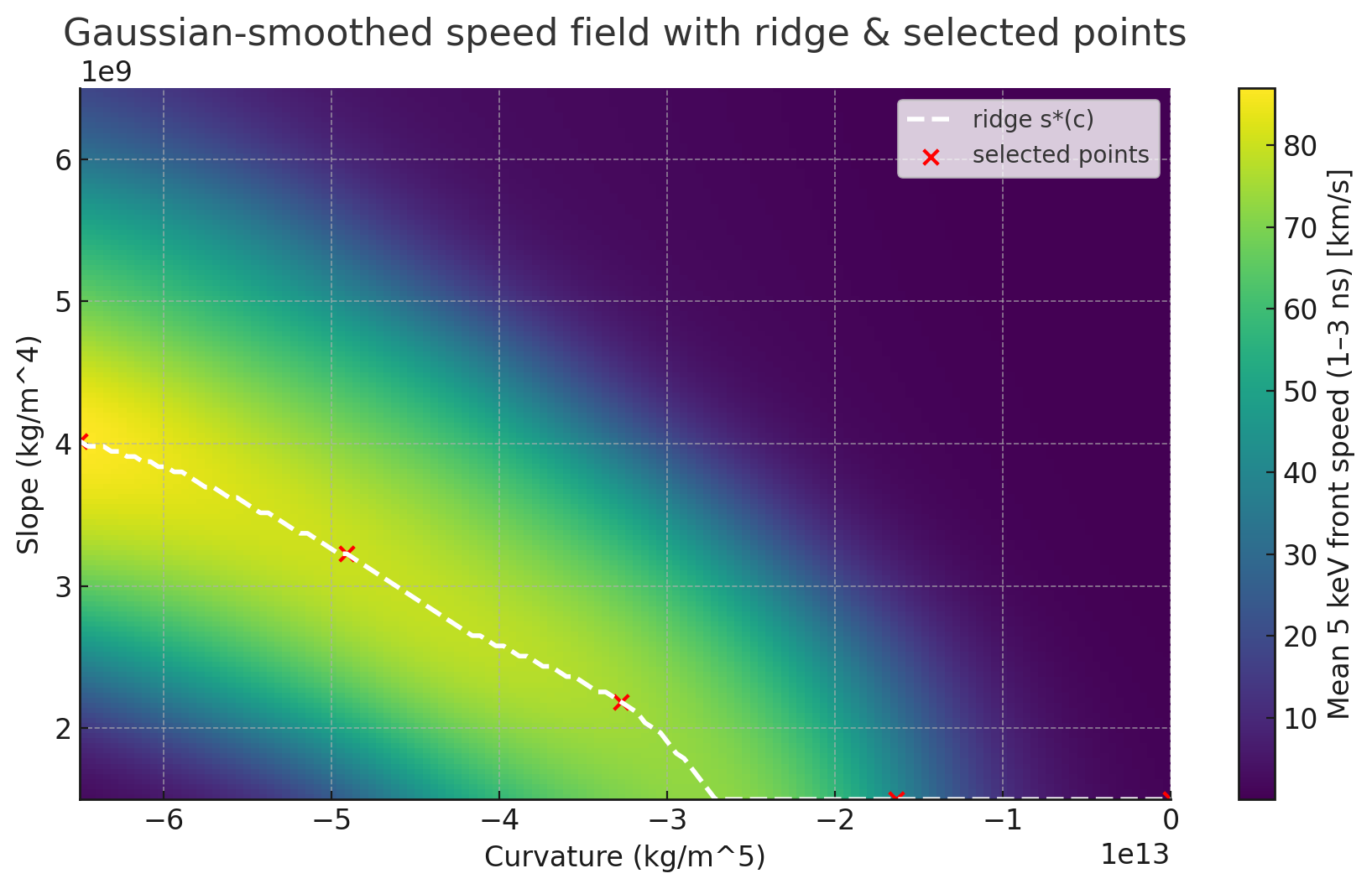
图 1:颜色图表示传播到冷 ICF 燃料中的热核燃烧波的平均传播速度。该波速取决于热冷 DT 燃料之间界面的轮廓。更具体地说,平均斜率和曲率都起着关键作用。它们共同设定了在给定物理假设下提供最高速度波的最优轮廓。这些最优轮廓沿着黄色脊线。
我们花了一些时间检查沿脊线的密度轮廓。选择了沿该脊线等距分布的五个点;它们的参数列于下表。
| # | 斜率 (kg/m⁴) | 曲率 (kg/m⁵) |
|---|---|---|
| 1 | $4.02 \times 10^{9}$ | $-6.5 \times 10^{13}$ |
| 2 | $3.23 \times 10^{9}$ | $-4.91 \times 10^{13}$ |
| 3 | $2.18 \times 10^{9}$ | $-3.27 \times 10^{13}$ |
| 4 | $1.50 \times 10^{9}$ | $-1.64 \times 10^{13}$ |
| 5 | $1.50 \times 10^{9}$ | $0$ |
图 1 说明,随着曲率变得不那么负,热斑边界附近的密度上升得更快——这加强了热耦合并略微降低了前沿速度。最优轮廓表现出温和的初始密度上升,允许 α 粒子在损失主导更深的冷燃料之前预热斜坡。
在几个小时的摸索中,我们对描述界面的参数与传播快速燃烧前沿的最优值之间的关系有了一个不错的数值图景。
理论解释
虽然数值显示了一个趋势,但一个好的设计物理学家会旨在使用他可支配的理论工具来解释这个趋势。我请求 GPT-5 在这里帮助做这件事有两个原因。首先,拥有这个理论图景对于形成我们正在寻找的直觉是有用的。其次,它提供了另一种检查,即 GPT-5 没有幻觉物理,而我没有被愚弄。这是一个非常需要的验证过程。
GPT-5 很快就确定了(在我的推动提示之后)一个行波功率平衡来理解是什么设定了脊线。
我们确定了一个准稳态燃烧前沿,写成随体坐标 $\xi=r-vt$。从施加的斜坡写 $\rho=\rho(\xi)$,能量方程读作
$$-v\,\rho C_v\,\frac{dT}{d\xi} = \frac{d}{d\xi}\left(\rho\,\chi(T,\rho)\,\frac{dT}{d\xi}\right) + Q_\alpha\bigl[T,\rho;\rho(\cdot)\bigr] - Q_{\mathrm{rad}}\bigl(T,\rho,\rho R_{\rm out}\bigr).$$
它识别出我认为正确的关键标度律:
- 热输运:$\chi \sim \chi_0 T^{5/2}/\rho$。低 $\rho$ 意味着强预热(大 $\chi$),但也意味着稀薄的热容量(较小的 $\rho C_v$)。
- 聚变源:$Q_\alpha \sim f_\alpha E_{\rm fus}(n_D n_T)\langle\sigma v\rangle(T)\,\mathcal{D}[\rho]$。由于 $n\propto\rho$,这给出 $Q_\alpha \propto \rho^2 \langle\sigma v\rangle(T)$ 乘以非局域沉积因子 $\mathcal{D}[\rho]$。
- 辐射损失:$Q_{\rm rad}\sim C_{\rm rad}\rho^2 \sqrt{T}/(1+\kappa_0 \rho R_{\rm out})$。更高的 $\rho$ 放大发射率但也增加光学深度并减少逃逸。
脊线(最大平均前沿速度)由这样的 $(s,c)$ 对组成:进入预热区的净功率——来自传导加 α 沉积——最有效地克服辐射损失和将冷燃料提升到 5 keV 点火阈值所需的焓。换句话说,在那里
$$\underbrace{\text{(来自热侧的传导)} + \text{(非局域 α 沉积)}}_{\text{有效驱动}} \;\;\;\text{相对于}\;\;\; \underbrace{\text{(辐射损失)} + \text{(下游传导)} + \rho C_v v \Delta T}_{\text{汇 + 焓}}$$
被最大化。
它论证了最优斜率 $s$。将斜坡(端点归一化)写成
$$\rho(\xi)\approx \rho_{\rm hs} + s\,\Delta + c\,\Delta^2,\quad \Delta\equiv (\xi-\xi_{\rm hs})\in[0,L_{\rm ramp}].$$
使 $s$ 更小(更浅):近前沿 $\rho$ 在更长的距离内保持较低。
- 优点:更大的 $\chi\propto 1/\rho$ 意味着更好的传导到达;更长的 α 阻止长度 $\lambda_\alpha\sim R_m/\rho$ 意味着 α 粒子在前沿前方预热。
- 缺点:$Q_\alpha\propto \rho^2$ 在前沿较弱;热预热层也光学上更薄,所以辐射逃逸改善。
使 $s$ 更大(更陡):前沿更快地看到更高的 $\rho$。
- 优点:更强的 $Q_\alpha\propto \rho^2$,更大的热容量 $\rho C_v$ 来"捕获和保持"热量,更大的 $\rho R$ 所以 α 能量更局部地沉积(更大的 $f_{\rm dep}$)。
- 缺点:$\chi$ 作为 $1/\rho$ 下降,所以预热更差;发射率($\propto\rho^2$)上升,给出更大的辐射汇(即使逃逸概率缩小)。
净效果:存在一个 $s$ 的最佳点,在那里传导/α 到达仍然良好,但前沿的 $\rho$ 刚好足够高以引导自加热而不会过度损耗。
然后它转向最优曲率 $c$ 以及为什么"适度负"值获胜。
曲率重新分配密度沿斜坡上升的位置:
- 负曲率($c<0$)在热斑边缘附近产生温和的初始上升,后来产生更陡的上升。这创建了一个"预热架":一个低 $\rho$、光学上更薄、高 $\chi$ 的区域,恰好在来自热斑的 α 沉积想要着陆的地方(几个 $\lambda_\alpha$ 之外)。它在损失接管之前增强了非局域 α 耦合和传导提升到斜坡中的 5 keV。
- 正曲率($c>0$)产生陡峭的早期上升,快速增加热斑外的 $\rho$。这扼杀了预热(低 $\chi$),增加发射率,并缩短 $\lambda_\alpha$,所以更多的 α 能量沉积在前沿后面而不是前面——对后面的峰值 $T$ 好,对前沿推进不好。
这就是为什么数据在几乎任何位于脊线上的斜率下都偏好适度负曲率:它在正确的距离上定位正确的 $\rho$,使得 α-传导协同作用在前沿需要的地方被最大化。
最终,一个简单的功率平衡准则预测每个 $s$ 的"理想"$c$。一个有用的心智模型是关注一个厚度为 $\delta$ 的控制体积,中心位于热斑边缘前方距离 $\Delta^\star$ 处,前沿正在那里形成。选择 $\Delta^\star\sim$ 几个局部 α 射程和 1-3 ns 期间的传导穿透深度。然后要求那里的净正功率以达到并保持 $T_{\rm ig}\approx 5\,\text{keV}$:
$$\underbrace{Q_\alpha^{\rm in}(\Delta^\star)}_{\text{来自热侧的非局域}} + \underbrace{Q_{\rm cond}^{\rm in}(\Delta^\star)}_{\propto \chi\,\Delta T/\ell} \gtrsim \underbrace{Q_{\rm rad}(\rho(\Delta^\star),T)}_{\propto \rho(\Delta^\star)^2 \sqrt{T}/(1+\kappa_0\rho R_{\rm out})} + \underbrace{\rho(\Delta^\star) C_v \frac{T_{\rm ig}-T_0}{\tau}}_{\text{时间尺度 }\tau\text{ 上的焓}}.$$
两个闭合关系将 $\rho(\Delta^\star)$ 连接到 $(s,c)$:
- α 射程:$\lambda_\alpha(\Delta^\star)\sim R_m/\rho(\Delta^\star)$ 应该与 $\Delta^\star$ 相当,否则 α 粒子要么超调($\rho$ 太低)要么沉积在后面($\rho$ 太高): $$\rho(\Delta^\star)\,\Delta^\star \sim R_m \quad\text{(面密度量级为一)}.$$ 对于固定的 $s$,这确定了一个 $\rho(\Delta^\star)$,从而通过 $\rho(\Delta^\star)=\rho_{\rm hs}+s\,\Delta^\star+c\,{\Delta^\star}^2$ 固定所需的曲率 $c$。
- 传导匹配:时间 $\tau$ 内的传导预热长度是 $\ell_c \sim \sqrt{\chi\,\tau}\sim\sqrt{(\chi_0 T^{5/2}/\rho)\tau}$。有效预热需要 $\ell_c\sim\Delta^\star$,即 $$\frac{\chi_0 T^{5/2}}{\rho(\Delta^\star)} \sim \frac{{\Delta^\star}^2}{\tau}.$$ 这再次在给定 $s$ 和 $\tau$(我们指标中的 1-3 ns)下固定 $\rho(\Delta^\star)$(因此 $c$)。
综合起来,对于每个斜率 $s$,存在一个最佳 $\rho(\Delta^\star)$,同时(i)匹配 α 面射程($\rho\Delta^\star \sim R_m$)和(ii)传导到达($\ell_c\sim\Delta^\star$)。因为 $c$ 是在保持斜坡端点固定的同时局部重塑 $\Delta^\star$ 处 $\rho(\Delta)$ 的自由度,你得到一个理想曲率 $c^\star(s)$。这个 $c^\star(s)$ 追踪观察到的脊线。
从该准则得到的直觉:
- 如果 $s$ 太浅,$\rho(\Delta)$ 保持较小;你需要一个不那么负的 $c$(甚至正的)来将 $\Delta^\star$ 处的 $\rho$ 提高到足以满足 $\rho\Delta^\star\sim R_m$。
- 如果 $s$ 太陡,$\rho(\Delta)$ 快速攀升;你需要更负的 $c$ 来延迟上升,以便 α/传导可以在损失激增之前到达并加热前沿前方。
因此,脊线曲率是 $\rho(\Delta^\star)$ 达到金凤花窗口的轨迹:对于 $Q_\alpha$ 和约束足够大,对于到达和低辐射消耗足够小。
我们还开发了测试,以确保我们清楚脊线应该如何随物理旋钮移动。
这幅图立即预测了如果你改变微观物理脊线如何移动:
- 更长的 α 射程 $R_m$:将最优推向更浅的 $s$ 和更负的 $c$(以保持 $\rho\Delta^\star \sim R_m$)。
- 更强的辐射(更大的 $C_{\rm rad}$ 或更低的不透明度):偏好前沿附近更浅的密度,所以在给定 $s$ 下更负的 $c$。
- 更低的热斑温度:减少源,所以最优向略大的 $s$ 移动(前沿形成处更多 $\rho$),但仍然偏好负 $c$ 以保持到达。
最后,我们以一个紧凑的"工程规则"结束。选择一个与你的时序窗口(例如 1-3 ns)和期望的 5 keV 穿越相关的目标预热距离 $\Delta^\star$。然后设计 $(s,c)$ 使得
$$\rho(\Delta^\star)\,\Delta^\star \approx R_m \quad\text{和}\quad \frac{\chi_0 T_{\rm ig}^{5/2}}{\rho(\Delta^\star)} \approx \frac{{\Delta^\star}^2}{\tau}.$$
这简化为对 $\rho(\Delta^\star)$ 的单一条件,因此在每个斜率 $s$ 下有一个曲率 $c^\star$。在实践中,你将落在具有适度负曲率的浅斜率上,正是模拟所强调的。
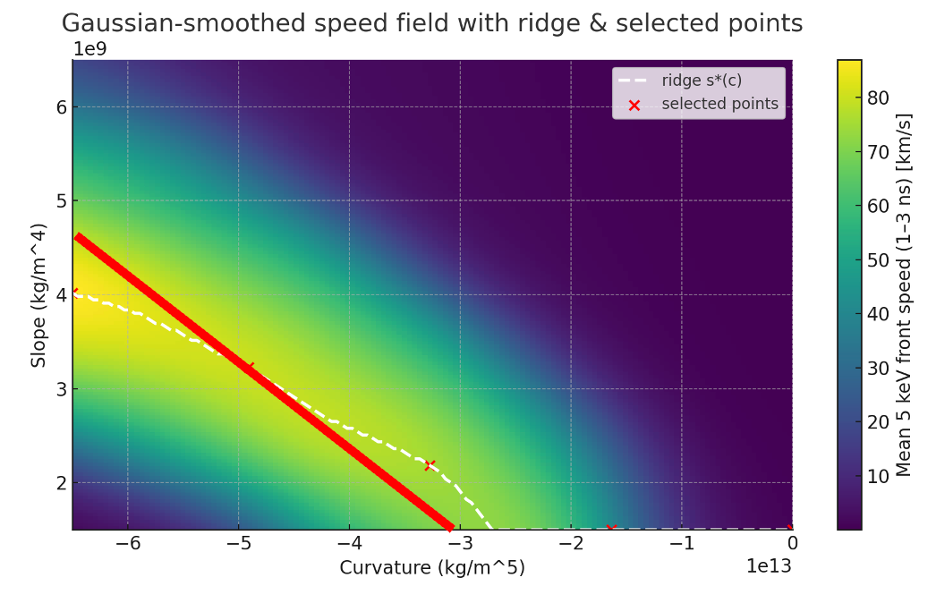
图 2:红线表示我们理论阐述所发展的理论脊线斜率。它与数值脊线相当吻合。数值结果与理论功率平衡论证验证的结合增加了对结果的信心。
这个公式使用微观物理和功率平衡来估计预期的 $c^\star(s)$ 关系,提供了对我们结果的检查。如图 2 所示,红色工程规则和数值获得的脊线相当接近。我在这个项目上投入了大约 6 小时(它相当有趣,但练习是要快),我最终得到了一个数值结果和一个理论解释,给了我继续进行的信心。正如我前面提到的,这个过程本身并不新颖。这是一个在 ICF 前沿领域工作的设计物理学家的工作流程。然而,在几小时内从概念执行到数值探索再到理论支持陈述是相当惊人的。
物理结论和研究成果
在开始时,我正在寻找一组物理目标,我们交付了:
- 静态的、一维球形反应-扩散模型捕获了 ICF 热斑点火和传播的基本燃烧波物理。
- 包括真实的 α 阻止和非局域沉积以及灰色辐射损失,产生可信的传播阈值(接近 1 keV 的边际点火)。
- 脊线分析识别出一系列燃料斜坡——浅斜率、适度负曲率——在固定 $T_{hs}$ 下最大化前沿速度。
- 理论分析从随体波前中的基本功率平衡解释了密度轮廓空间中的脊线。
- 得到的框架作为物理知情的测试平台,用于发展理论、验证更高保真度的流体动力学模拟和设计未来实验。
这是我使用 GPT-5 的代表性体验。模型采纳了我有的想法种子——一个静态模型来感受热核燃烧波启动和传播的关键物理——并帮助我非常快速地构建了模型的偏微分方程表示。根据指令,它纳入了 ICF 社区已知的详细阻止本领和熟悉的(对专家来说)物理数据。它离散化了问题,设置了我想象的优化程序,并交付了我认为我们会期望的结果。这从开始到完成花了我大约 6 小时——从想法到写作。没有太多专业知识是我不能通过询问国家实验室的同事、进行互联网搜索、手工推导一些东西、回忆一些本科和研究生的数值技巧以及编写几百行代码找到的。而且,这太神奇了。它让我成为一个人的专家军团,就好像我曾经在我想过的关于 ICF 的一切上处于最佳状态。我可以说出它感觉像在与之交谈的世界专家的名字,或者我必须联系以帮助我完成某个小步骤的人。但是,他们就在我的笔记本电脑里(或多或少)。
我与它一起制定的理论解释可能是最好的部分。这个解释直接将已知的物理关系联系在一起,给出我们已经发现的东西的闭式预测器。这是确保在与模型数小时引出中构建的结果没有错误的好方法,而且模型没有诱惑我购买它的论点。
我必须说,结果并非没有工作。模型在急于取悦中,经常引入数值胶带来平滑棘手的问题,悄悄地用它知道我想要的趋势的近似替换详细的数值求解,并在数值信号仍然明显是噪声时自信地宣布胜利。当指出这些错误和不想要的结果时,模型非常擅长实际修复问题。但是,用户必须足够专家才能捕捉过度简化,必须坚持让模型重新考虑,并且必须保持警惕以确保精炼的结果朝着正确的方向发展。
总体而言,正如我多次指出的,我觉得我在这里的 6 小时工作产出了我可以用一对非常好的博士后——一个做理论一个做数值——在一两个月内完成的东西。所以,大约 6 个人月减少到 6 个人小时。这是大约 1000 倍的压缩。我只能想象如果两个博士后和我合作,我们每个人都以这种 AI 加速模式工作会怎样。
IV. AI 获得的新科学成果
IV.1 Erdős 问题(第 2/2 部分)— Mehtaab Sawhney 和 Mark Sellke
我们从第 II.2 节离开的地方继续,解释 GPT-5 Pro 如何帮助我们解决 Erdős 问题 #848。
AI 辅助求解问题 #848
Erdős 问题 #848 属于组合数论领域,作为问题 23 发布在 Erdős 1992 年的论文中。这个问题是真正开放的,现在已由第一作者和 GPT-5 合作解决,结合了 van Doorn、Weisenberg 和 Cambie 的在线评论。问题陈述如下:
问题 #848:设 $A$ 是 $\{1,2,\dots,N\}$ 的子集,使得对于所有 $a,b\in A$,$ab + 1$ 不是无平方因子数(即 $ab+1$ 必须被至少一个素数 $p$ 的 $p^2$ 整除)。那么对于所有足够大的 $N$,这样的集合 $A$ 的元素数量不超过 $A = \{1\leq a\leq N: a\equiv 7 \pmod{25}\}$。
当然,给定的集合 $A$ 满足所需性质,因为 $7^2+1\equiv 0 \pmod{25}$。进一步证明,这个最大的 $A$ 是唯一的,除非 $\{1\leq a\leq N: a\equiv 18 \pmod{25}\}$ 具有相同的大小,并且对于某个 $\varepsilon>0$,任何包含至少 $\frac{(1-\varepsilon)N}{25}$ 个元素的 $A$ 必须包含在这两个中的一个里。
解决方案的出发点是观察到对角约束($a^2+1$ 不是无平方因子数)已经对 $A$ 施加了实质性限制。事实上,经典数论表明只有形如 $p\equiv 1\pmod 4$ 的素数才能两次整除 $a^2+1$,对于每个这样的素数,只有 $2/p^2$ 比例的整数 $a$ 使得 $a^2+1$ 被 $p^2$ 整除。由于不同素数幂的整除性表现近似独立,这已经给出了简单的上界:
$$1-\prod_{\substack{p \text{ 素数},\\ p\equiv 1\text{(mod 4)}}}\Big(1-\frac{2}{p^2}\Big) \approx 0.105$$
这与真实值相差在 3 倍以内。
更具挑战性的是利用 $ab+1$ 的非对角约束来非平凡地改进这个上界。为此,第一作者向 GPT-5 Pro 询问建议。GPT-5 的回复中建议的想法给出了一种方法,使用任何单个数 $b\in A$ 来对所有其他 $a\in A$ 获得类似苛刻的约束。
例如,设 $A^{\ast}$ 为 $A$ 中既不等于 7 也不等于 18 模 25 的数组成的子集。如果 $A^{\ast}$ 非空,那么固定任何 $b\in A^{\ast}$,对于任何 $a\in A$,$a^2+1$ 或 $ab+1$ 必须被某个素数 $p$ 的 $p^2$ 整除。但由于 $b\in A^{\ast}$,只有其中一个可以被 5 本身整除。这对 $a\in A$ 是一个更强的限制,已经给出了改进的界:
$$\Big(\frac{23}{25}\Big)\Big(1 - \prod_{\substack{p\equiv 1\pmod 4\\p\ge 13}}\Big(1-\frac{2}{p^2}\Big)\Big) + \frac{2}{25}\Big(1 - \prod_{\substack{p\neq 5}}\Big(1-\frac{1}{p^2}\Big)\Big) \le .02517 + .0294 \approx .05457$$
这个界已经不远离真实值,这表明进一步推进它应该能解决整个问题。GPT-5 在这个方向上做出了尝试,但在实现中有许多错误。尽管如此,高层次的想法是正确的,并很快被转化为完整的证明。
最终证明的第一步是注意到,如果 $b\in A^{\ast}$ 而且是偶数,那么 $ab+1$ 不能被 4 整除,所以上面的界改进为约 0.03767。由于 $0.03767 < 1/25$ 严格小于 7 模 25 的数的密度,这已经意味着一个近最大集合 $A$ 根本不能包含 $A^{\ast}$ 中的任何偶数。进一步的分情况讨论允许排除任何 $b\in A^{\ast}$ 的存在,最后证明 7 和 18 模 25 之间的混合也是低效的。
我们强调,第一个提到的观察归功于 Wouter van Doorn,给 GPT-5 的特定提示词基于 Stijn Cambie 的评论;这些已经存在于官方网站的评论中。因此,最终证明由一个关键的 GPT-5 解决步骤夹在两层人类数学之间!
展望
我们对 Erdős 问题 #848 的调查突显了 GPT-5 有能力作为有效的数学助手,能够回忆相关引理、识别类比并从模糊、不明确的提示词中定位相关结果。然而,当前模型在感知数学的"负空间"方面仍然有限。虽然模型能够建议合理的证明策略,但它们往往没有意识到某些"明显"的例子阻碍了进展,并且对现有方法的力量过于自信。这并不令人惊讶,因为这种讨论在数学文献本身中大多是缺失的;数学家并不系统地记录为什么问题超出了能力范围,或者为什么更明显的策略不起作用,或者为什么某些技术本质上无法解决某些类别的问题。
IV.2 在线算法新下界 — Christian Coester
本节描述 GPT-5 如何帮助证明在线优化中一个基本问题——凸体追逐算法性能的新界限。这个问题由 Friedman 和 Linial (1993) 引入,捕捉了在不确定性下如何做出顺序决策,当每一步以几何方式限制可行选项时。
形式上,给定一个凸集序列 $K_1, K_2, \ldots, K_T\subset \mathbb{R}^d$,逐一揭示。在看到 $K_t$ 后,算法必须在学习下一个集合之前选择一个点 $p_t \in K_t$。目标是最小化总移动量 $\sum_{t=1}^T \|p_t - p_{t-1}\|$。该算法被称为在线算法,因为它必须即时做出决策,而不知道未来。
在线算法的标准性能度量是其竞争比,定义为任何实例上在线算法成本与最优(离线)成本之间的最坏情况(即最大)比率。
跟随领导者算法的下界
当初始位置是 $p_0=0$ 时,观察到对于嵌套凸体追逐,最优离线算法会移动到 $\arg\min_{p\in K_T}\|p\|$,这对所有时间步都是可行的并且最小化成本。所以一个自然的在线算法是在每个时间 $t$ 移动到 $p_t = \arg\min_{p\in K_t}\|p\|$,即跟踪当前最优的离线位置。
给定一个简短的提示词,GPT-5 产生了一个相当非显而易见的反例来反驳这个算法:
考虑二维欧几里得空间中的嵌套凸体追逐,其中初始位置是 0,初始凸体是以 0 为中心的单位球。证明或反驳跟随领导者算法(即始终移动到当前凸体中范数最小的点)的成本最多是 π/2。
[推理了 16 分 19 秒]
简短回答:该陈述是错误的。
GPT-5 然后构造了一个交替构造,使用角度序列 $\{\varphi_m\}$ 满足 $\sum_{m=1}^\infty \varphi_m = \infty$ 且 $\sum_{m=1}^\infty \varphi_m^2 < \infty$,证明贪婪成本可以变得任意大,同时所有请求都保持嵌套在单位圆盘内。
一般算法的改进下界
我们现在讨论 GPT-5 的帮助如何证明任意在线算法竞争比的更好下界。下界的想法基于 Bienkowski 等人 (2019) 之前对追逐线(即每个 $K_t$ 是一条线)的 1.5358 下界。
下界想法:考虑一个实例,初始位置 $(0,0)$,每个请求集是一条线,最初是线 $y=0$。开始绕 $B=(1,0)$ 顺时针旋转线。由泰勒斯定理,原点在当前线 $K_t$ 上的投影 $p_t$ 是 $K_t$ 与以 $(1/2,0)$ 为圆心、半径为 $1/2$ 的圆的西北交点。如果在线算法沿着这条曲线直到请求线变成垂直,那么它沿半圆移动,其成本恰好是 $\pi/2$,而最优成本是 1。
GPT-5 建议了一个更简单、更干净的解决方案来处理证明中的技术问题:当算法在半圆以下且与 $p_t$ 的距离 $\ge \epsilon$ 时触发切换。这避免了冻结问题,当 $\epsilon\to 0$ 时我们获得相同的 $\pi/2$ 下界。
扩展到更高维度:最后,GPT-5 提出了一种产生 $\frac{\pi}{2} \sqrt{\lfloor \frac{d}{2}\rfloor} \approx 1.11\sqrt{d}$ 下界的方法。想法很简单:考虑 $\mathbb{R}^d$ 到 $\lfloor d/2\rfloor$ 个二维分量 $\mathbb{R}^2$ 的正交分解,然后在各分量中逐一应用 $\pi/2$ 下界。
反思
GPT-5 在这个问题的研究过程中在几个阶段提供了帮助。也许最令人印象深刻的部分是它反驳跟随领导者算法的证明,从单个提示词产生,没有任何关于如何处理任务的指导。这个结果节省了我可能花在无果地搜索上界的大量时间,而且不清楚我是否能够想出这个下界,它包含了几个非平凡的步骤。
IV.3 树中子图计数不等式 — Sébastien Bubeck, Mark Sellke 和 Steven Yin
我们在这里进行另一个实验,这次是在图论中,关于本节第一作者与 Nati Linial 在 2013 年预印本中制定和研究的问题(后于 2016 年发表在 Journal of Graph Theory)。
树中的路径、星和 Y 形图
设 $G$ 是一棵有限树。我们考虑以下子图计数:
- $S$ 是 $G$ 中 5 顶点诱导星子图的数量。
- $P$ 是 $G$ 中 5 顶点诱导路径子图的数量。
- $Y$ 是 $G$ 中剩余同构类型的诱导 5 顶点子树的数量(即 1 个中心顶点是长度为 1,1,2 的路径的端点)。
定理 (Bubeck-Linial 2016):对于任何有限树 $G$,有 $Y-9S-P\leq 6$。
猜想:存在某个常数 $K>0$,使得对于任何有限树 $G$,有 $29Y-42P-144S\leq K$。
在某种意义上,定理给出了这个凸集的"第一面",而猜想给出了"第二面"。
GPT-5 的新证明
我们向(配备脚手架的)GPT-5 提出问题后,它能够:
- 重新证明第一个定理:使用与 2016 年人类证明完全不同的方法,基于一个"奇迹般的恒等式",整个论证只需一页半。
- 证明第二个(开放)猜想:确认了 $C=2$ 的情况是正确的,证明了 $29Y-42P-144S\leq 504$。
关于第一个定理的证明,关键身份是:
$$Y-9S-P = \sum_{v\in G}\Big[F(d_v) -\frac{(T_v-A_v)^2}{2}\Big]$$
其中 $F$ 是四次多项式,$d_v$ 是顶点 $v$ 的度,$T_v$ 是相邻顶点度数之和。GPT-5 发现了一个"奇迹般的恒等式",使得余项的求和可以伸缩消除或保持非正,从而完成证明。
除了被检查和为清晰度重写外,下面的新证明完全由 AI 生成。
值得注意的是:
- GPT-5 在这个实验中没有访问网络搜索,似乎不知道 2016 年论文中的现有证明
- 预先存在的(人类生成的)证明依赖于相当繁琐的分析,跨越 4 页计算分析几种不同情况
- 相比之下,GPT-5 的证明简短而优雅,基于一个有些神奇的恒等式
IV.4 动态网络上的 COLT 问题 — Sébastien Bubeck, Mark Sellke 和 Steven Yin
我们考虑一个随机树 $(G_t)_{t\ge1}$,按以下方式迭代构造。在时间 $t=1$ 时,我们从单个顶点开始。在每个后续时间 $t+1$,添加一个新顶点 $Y_{t+1}$ 并按照下面描述的随机优先连接规则连接到现有的父顶点 $X_{t+1}\in\{Y_1,\dots,Y_t\}$。
每个顶点 $v$ 独立地接收一个永久的"吸引力"标签 $a(v)\in\{1,w\}$,两个选项的概率相等。顶点 $x$ 的吸引力加权度为 $A_t(x) := \sum_{y\sim_t x} a(y)$。父顶点 $X_{t+1}$ 按照以下方式选择:
$$\mathbb{P}(X_{t+1}=x\mid \mathcal{F}_t) = \frac{A_t(x)}{S_t},\quad S_t := \sum_{x\in V_t} A_t(x)$$
我们的目标是基于单个大 $t$ 值时的 $G_t$,在不观察顶点标签的情况下近似恢复 $w$。这作为 2012 年学习理论会议(COLT)的开放问题提出。
考虑一个修改的优先连接树过程,其中每个顶点也带有一个 $\{0,1\}$ 中的标签,均匀随机选择。标签为 1 的顶点的"吸引力"是 $w>0$,标签为 0 的是 1。顶点的"吸引力度"定义为其邻居吸引力之和。当添加新顶点时,它以与现有顶点吸引力度成比例的概率连接到该顶点。基于对由此过程生成的大型无标签树的观察,是否可能识别 $w$?要么给出一个算法来做到这一点,要么证明信息论上的不可能性。
GPT-5 能够证明 $w$ 确实是可识别的,通过计算在给定大时间时叶子顶点的极限比例 $f(w)$:
定理:对于任何 $w>0$,几乎必然有:
$$\lim_{t\to\infty}\frac{L(t)}{t} = f(w) \equiv \frac{3}{4}-\frac{1}{2(w+2)}+\frac{1}{4(2w+1)} = \frac{3(w+1)^2}{2(w+2)(2w+1)}$$
函数 $f$ 容易看出是严格递增的,从 $f(1)=2/3$ 增加到 $\lim_{w\to\infty} f(w)=3/4$。$w$ 的可识别性是直接的:点估计 $\hat{w}(t)=f^{-1}(L(t)/t)$ 当 $t\to\infty$ 时概率收敛到 $w$。
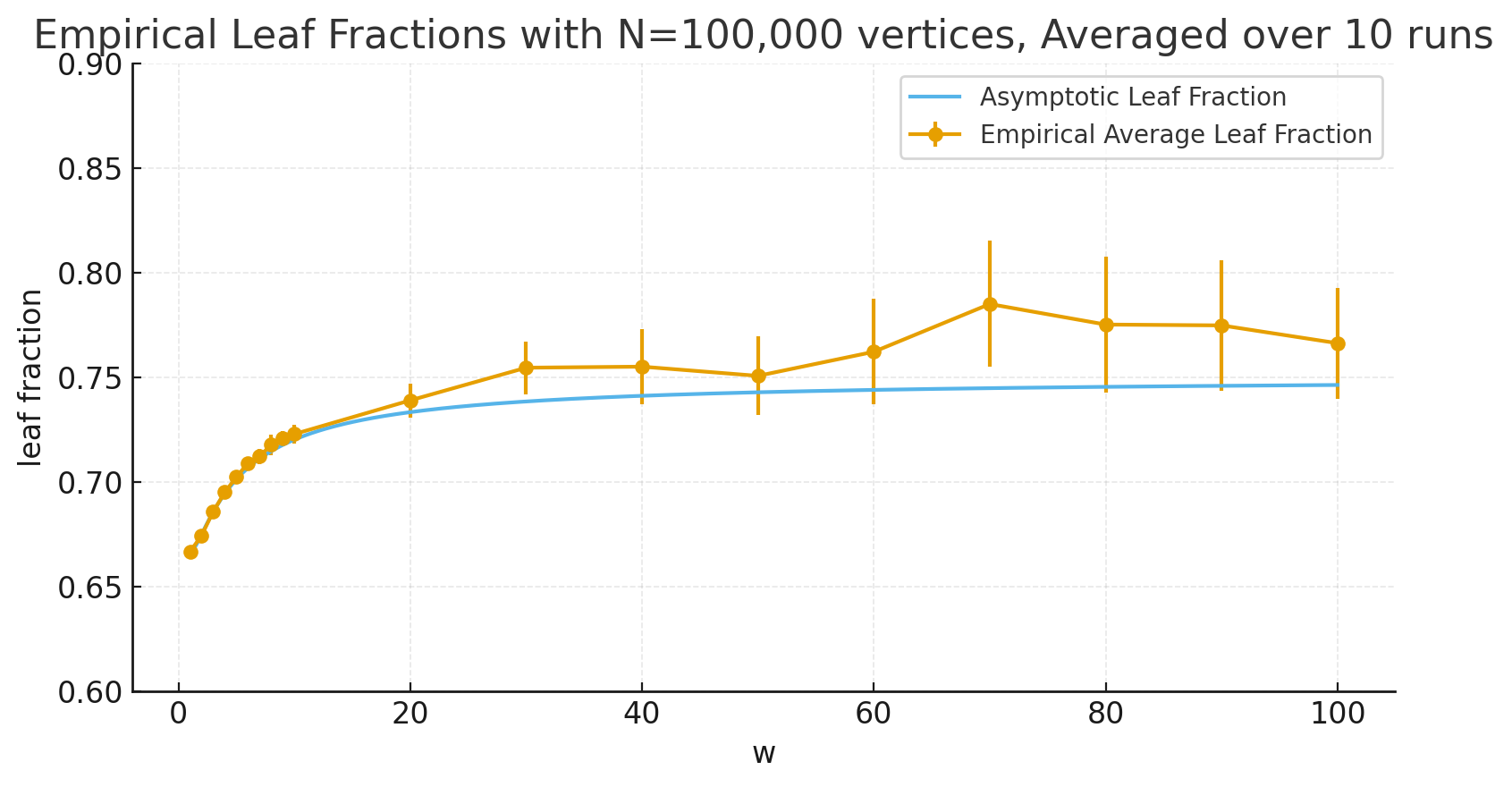
定理中渐近结果的模拟。橙色图显示 $G_{10^5}$ 中叶子比例的平均值(和经验标准差),跨越每个 $w$ 的 10 次独立试验。函数 $f(w)$ 在 $w\in [1,\infty)$ 上用蓝色绘制。生成此图的代码由 GPT-5 编写。
值得注意的是,GPT-5 决定关注数量 $L(t)$ 已经是非显而易见的——在一个相关模型中,这种类型的算法被证明会失败。
虽然所有主要证明思想归功于 GPT-5,但有些证明写作细节是人类提供的。我们的脚手架版 GPT-5 自主产生了完全相同的高层次论证和相同的主要参考文献,但省略了某些中间断言的证明细节,声明(正确地)它们来自常规随机近似论证。
结论
AI 模型因协助日常任务而闻名;不太为人所知的是,像 GPT-5 这样的前沿模型越来越能够加速新颖的研究。我们重点介绍了跨越一系列科学学科的例子,展示 GPT-5 在构思、支持深度文献搜索,甚至提出和实现(适当规模的)开放问题的证明方面的帮助。这一切在仅仅十二个月前都是不可能的。GPT-5 已经显示出它可以加速科学研究这一事实,结合前沿 AI 的改进速度,表明未来几年将是科学和数学令人振奋的时代。
致谢
A. Lupsasca 部分由国家科学基金会通过 CAREER 奖 2340457 和拨款 2307888 资助,以及西蒙斯基金会通过拨款 SFI-MPS-BH-00012593-09 资助。本研究是在 M. Sawhney 担任 Clay Fellow 期间进行的。C. Coester 由欧盟(ERC, CCOO, 101165139)资助。表达的观点和意见仅代表作者本人,并不一定反映欧盟或欧洲研究委员会的观点。欧盟和资助机构均不对此负责。D. Unutmaz 感谢 Oral Alpan 医学博士对本报告第 3 节的批判性阅读。